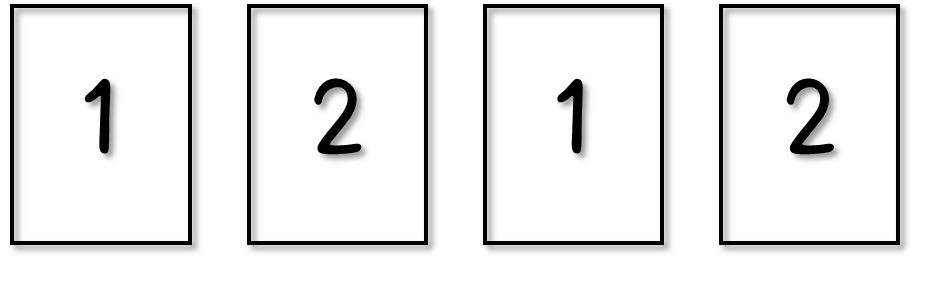みなさん、こんにちは。受験Dr.の桑田陽一です。
3月の講師ブログをお届けします。
本日は2023年3月2日。
8桁の数字で表すと「20230302」。0が3個、2が3個に3が2個。
3種類の数字しか使われていない日付だということに気がつきました。
そこで今回は、本日の日付にちなんだ場合の数の問題を考えてみましょう。
新6年生向けの問題ですが、今の時期には難しく見えると思います。
でも、根本原理を含んだシンプルな例題から順に進んでいけば、きっと理解できます。
算数好きな人は、ぜひ頑張って取り組んでみてください!
問題
0を3個、2を3個、3を2個使ってできる8桁の整数について考えます。
(1)このような整数は、全部で何個ありますか。
(2)このような整数のうち、20230302は小さい方から数えて何番目ですか。
「樹形図を使って書き出してみる」のでは大変そうです。
このように、同じものを何個か含むグループを並べるときの考え方、塾やクラスによっては5年でも触れていると思いますが、まだ不慣れな人がほとんどのはずです。
そこで、準備として、まずはもう少しシンプルな例題から考えてみましょう。
例題1
「1」のカードが2枚、「2」のカードが2枚あります。これらの4枚のカードを並べてできる4桁の整数は、全部で何通りありますか。
これなら「見覚えがある!」という人もたくさんいるでしょうか。
カードが少ないので樹形図を書いてみても良いのですが、今回は違う考え方を確認します。
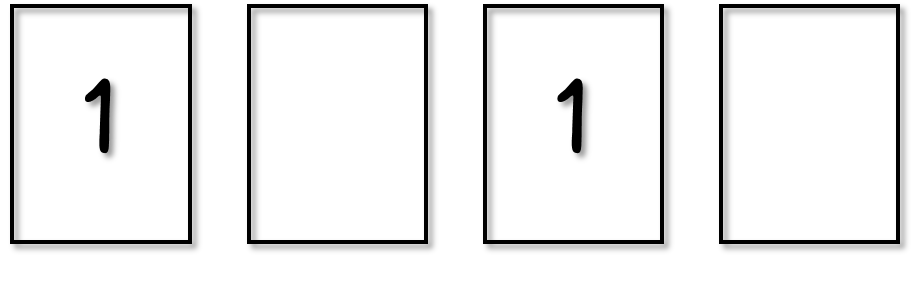
カードは全部で4枚。まずは、下のようにカードが入る「4つの空き枠」を考えます。
ここに、まずは「1」のカードだけを入れることにします。「1」のカードは2枚あるので、4つの枠から2つを選んで、カードを入れます。
全部で6通りの選び方がありますね。
実は、上のように書き出さなくても、4つの空き枠から2つの枠を選んでいるのですから、「選び方」の公式で、(4×3)÷(2×1)=6通りと求めることができます!
さて、「1」のカードは入れ終わったので、「2」のカードの入れ方を考えます。
例えば、「1」のカードがこのように入っているときは…。
残っている空き枠は2つ。2枚の「2」のカードは、この空き枠にそのまま入れるしかありませんね。
「1」のカードの入れ方6通りに対して、「2」のカードの入れ方は1通りずつ。ということは、結局4枚のカードのならべ方は6通りということになります。
このように、同じものが複数入ったグループを並べるときには、「並べ方」ではなく、「選び方」の考えを使います。
まず並べる枠を考え、空き枠からカードの入る場所を「選ぶ」という風に考えるのです。
例題2
「1」のカードが1枚、「2」のカードが2枚、「3」のカードが3枚あります。これらの6枚のカードを並べてできる6桁の整数は、全部で何通りありますか。
カードが増えましたが、基本の考え方は同じ。
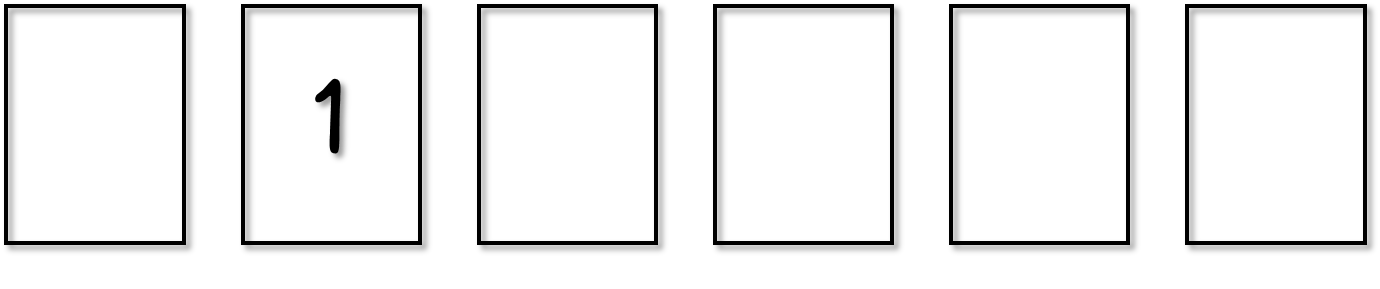
例題1と同じように、まずは「6つの空き枠」を考えましょう。
ここに、まずは「1」のカードを入れることを考えます。1枚しかないので、6通りの入れ方があります。
例えば、このように「1」のカードを入れたとします。
次は「2」のカードを2枚入れます。
空き枠は5つ残っています。ここから2つを選んでカードを入れることになりますね。
5つから2つを選ぶ方法は、(5×4)÷(2×1)=10通りです。
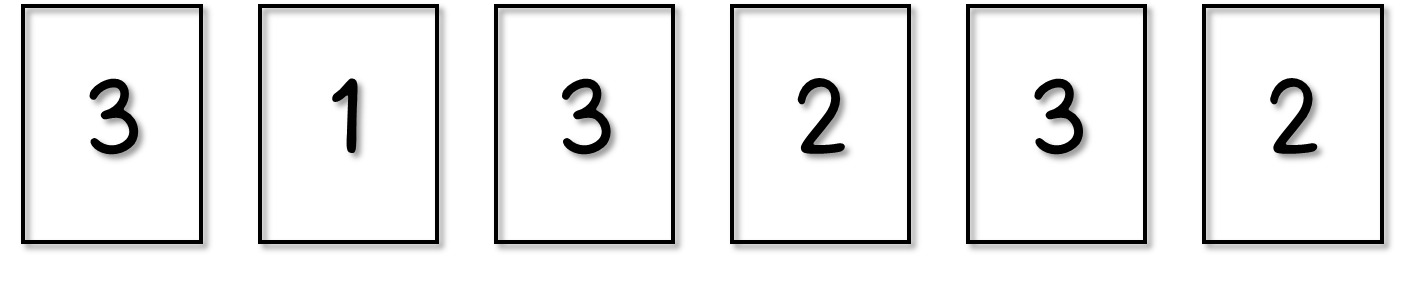
「2」のカードも仮にこう入れてみました。最後に「3」のカード3枚を入れるのですが…。
これは選ぶまでもなく、残った3つの枠にそのまま入れるしかありません。
以上をまとめると、「1」のカードの入れ方が6通り、このそれぞれに対して「2」のカードの入れ方が10通り。最後の「3」のカードの入れ方は1通りしかありませんので、6×10=60通りが答えだと分かりました!
さて、これで準備が整いました!元の問題を考えてみましょう。
解説
(1)
例題2と同じように考えたいところですが、0は一番上の位には使えないことに注意が必要です。
一番上の位に使える数字は、2か3。
①一番上の位の数字が2の時
2□□□□□□□の7つの□に入れる数字を考えます。
0が3個、2が3個、3が2個のうち、一番上の位に2を1個使いました。
残っているのは、「0が3個、2が2個、3が2個」です。
個数の少ない2と3から入れていきます。
2の入れ方は、7つの空き枠から2つを選ぶので、(7×6)÷(2×1)=21通り。
次に3の入れ方は、残り5つの空き枠から2つを選ぶので、(5×4)÷(2×1)=10通り。
最後に0は、残った空き枠に自動的に収まります。
よって、21×10=210通りの入れ方があります。
②一番上の位の数字が3の時
3□□□□□□□の7つの□に入れる数字を考えます。
残っている数字は、「0が3個、2が3個、3が1個」です。
個数の少ない3から入れます。
3の入れ方は、7つの空き枠から1つを選ぶので7通り。
次に2の入れ方は、残り6つの空き枠から3つを選ぶので、(6×5×4)÷(3×2×1)=20通り。
0は、残りの3枠に自動的に収まります。
数字の入れ方は、7×20=140通り。
①と②を合わせて、210+140=350通りが答えです!
(2)
これは難しいと思いますので、考え方のヒントを。
「20230302」までで作れる8けたの数を、小さい順に考えていくと…
①200□□□□□
①の形の数は、すべて20230302よりも小さい数です。
さらに、
②2020□□□□
③2022□□□□
②③の形の数も、20230302より小さいですね。
①②③の数がそれぞれ何個あるのかは、これまでの考え方を使って求めることができます。
あとは、
④2023□□□□
この形の数のうちで、20230302が何番目かを考えれば答えが求まります。
ここまで読み進めてくれた意欲のある人は、ぜひ自分で答えを出してみましょう。
…
…
…
…
…
この後は、敢えて簡潔に解説と答えを。
①の形の数は30個、②の形の数は12個、③の形の数は6個あります。
さらに④の□□□□に当てはまる数を小さい順に書き出すと、0023、0032、0203、0230、0302…となって、0302は5番目。
よって、求める答えは30+12+6+5=53番目です。
今回扱った考え方は、6年前期から夏期にかけて、本格的に学習するケースが多いかと思います。初めて見たよという人は、頭の片隅に入れておいてくださいね。