比の学び始めに意識しておくこと～5年算数～

みなさん、こんにちは。受験Dr.の桑田陽一です。
8月の講師ブログをお届けします。

夏期講習も後半戦。5年生のみなさんは、この夏で比を学び始めた人が多いでしょう。
今回は、比の学び始めのこの時期に、ぜひ意識してほしいことをお伝えします。

まずは、例題から。

例題

太郎くんの所持金は、花子さんの所持金の4/7です。

(1)花子さんの所持金が3500円のとき、太郎くんの所持金はいくらですか。
(2)太郎くんの所持金が840円のとき、花子さんの所持金はいくらですか。

簡単だ！と思った人が多そうです。
この問題、割合の考え方を用いると、普通は以下のように解きます。
分かっている人は、軽く読み流してもOK！

(1)
問題の条件から、
(太郎くんの所持金)＝(花子さんの所持金)×4/7なので、
(太郎くんの所持金)＝3500円×4/7＝2000円。

(2)
(太郎くんの所持金)＝(花子さんの所持金)×4/7より、
(花子さんの所持金)＝(太郎くんの所持金)÷4/7と表せます。
よって、
(花子さんの所持金)＝840円÷4/7＝1470円。

このように解ければ、もちろん問題なし！
でも、これまでの割合の学習を通じて、「かけるんだっけ？それとも割るんだっけ？」と、迷ってしまいがちだった人もいるでしょう。

実は、比を学んだことで、これからはそんな迷いから解放されます！

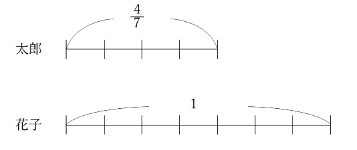
「太郎くんの所持金は、花子さんの所持金の4/7」という条件を、線分図で表すとこんな感じ。

4/7とは、「7つに分けたうちの4つ分」ということですから、上のような線分図で表せます。

これは、つまり…

そう、太郎の所持金：花子の所持金＝4：7ということですね。

「太郎の所持金は、花子の所持金の4/7」というのは、比を使って言いかえると、「太郎の所持金：花子の所持金＝4：7」ということなのです。

改めて、比を使って解いてみると…

(1)
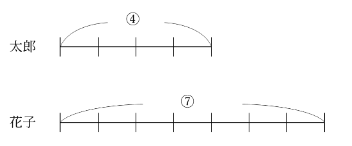
問題の条件から、太郎の所持金＝④、花子の所持金＝⑦と表せるので、

花子の所持金＝⑦＝3500円より、
①＝3500円÷7＝500円。
太郎の所持金＝④＝500円×4＝2000円。

(2)
太郎の所持金＝④＝840円より、
①＝840円÷4＝210円。
花子の所持金＝⑦＝210円×7＝1470円。

(1)も(2)も、同じ見方で解くことができました！

このように、比を学んだら、「割合の分数は比に直して扱う」というのが、多くの問題を統一的な視点で解くためのコツです。

もう1題だけ考えてみましょう。

AさんとBさんはそれぞれカードを何枚か持っていて、Aさんのカードの枚数はBさんのカードの枚数の25％です。

(1)AさんのカードとBさんのカードの枚数の合計が60枚のとき、Bさんのカードの枚数は何枚ですか。
(2)AさんのカードとBさんのカードの枚数の差が15枚のとき、Aさんのカードの枚数は何枚ですか。

割合の考え方でも解けますが、ぜひ意識して比を使って解いてみましょう。

25％＝25/100＝1/4。
つまり、「Aさんのカードの枚数はBさんのカードの枚数の1/4」。
さらに比を使って言いかえると、「Aさんのカード：Bさんのカード＝1：4」ということです。

(1)
Aさんのカード＝①、Bさんのカード＝④と表せるので、
①＋④＝⑤が60枚にあたります。
①＝60枚÷5＝12枚。
よって、Bさんのカードの枚数は④＝12枚×4＝48枚です。

(2)
④－①＝③が15枚にあたります。
①＝15枚÷3＝5枚。
よって、Aさんのカードの枚数は5枚です。

夏期が明けた9月以降は、図形や速さなど、他の分野への比の応用を学んでいくことになります。
そのときにも、今回紹介した「割合の分数→比に直して使う」という考え方は、基本的ながら大変重要。
ぜひ今のうちに慣れておきましょう！

今回はここまで。