こんにちは。
受験Dr.の松本　佳彦です。

突然ですが、問題です。

「個包装のクッキーが1万枚入っている箱があります。このうち100枚はチョコチップクッキー、残りはすべてプレーンクッキーです。なお、クッキーの包装は全て同じで、外からは判別できないものとします。
ある人が発明した機械を使うと、包装を開けることなく、常に99%の正確さで、そのクッキーの中身を当てることができます。つまり、この機械でチョコチップクッキーを100回検査すると、99回は正しく『チョコチップクッキー』という結果が出て、1回は誤って『プレーンクッキー』と判定されます。
今、箱の中からクッキーを1枚取り出し、この機械で検査すると、『チョコチップクッキー』と判定されました。
このクッキーは、本当に『チョコチップクッキーである』と言えるでしょうか。」

一見すると、正確さが99%というのはかなり信頼できる値であり、その機械が「チョコチップクッキー」と判断したのだから、これは間違いなくチョコチップクッキーである…と言えそうです。
しかし、この「正確さが99%」、即ち「1%外れる」というのが、算数では非常に曲者です。
今回は、「1」という小さい数が持つ、思いがけなく大きな力についてご紹介したいと思います。
（上の問題は「ベイズ推定」と呼ばれ、ウイルスの検査を例として語られることが多い問題です。中学入試でも2023年度の浅野中学校で出題されたテーマです。答えについては後述します）

❶角度が1°変わると？

「合同な三角形」の描き方については、小学校6年生で学習します。
うち、「2辺の長さとその間の角の大きさ」「1辺とその両端の角の大きさ」を用いて作図する場合、分度器を使用して三角形を描くことになります。
このとき、もし角度が1°ずれているとどうなるでしょうか。例えば、「底辺の長さが4㎝、両端の角度が30°と90°」という三角形を描こうとして、「30°」ではなく「31°」に合わせて描いてしまうと……。

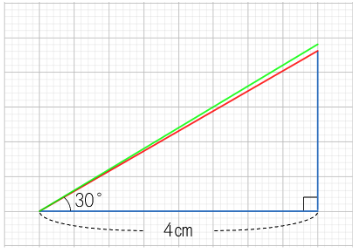
図のようになります。（赤線…30° 緑線…31°）右端に約1㎜の差が生じました。1㎜と聞くと小さく感じますが、実際に図にして、目盛りを重ねてみると差は歴然です。
底辺が長くなればなる程この差は大きくなり、仮に底辺が1㎞の長さになると、右端の差は約23.5ⅿまで広がります。
図が正確に描けていないことで、全体像が正しくつかめなかったり、試験で減点されたりと、様々な弊害が起こり得ます。
ですので、1°のずれ、1㎜の違いにも気を配り、丁寧に図を描くようにしましょう。

❷1分間で出来ること

「試験終了1分前です」というアナウンスがあると、何を考えるでしょうか。
「最後に答案を見直す」という話はよく聞きますが、1分ではとても見直す時間がない…と思ってしまうかもしれません。
しかし、計算問題の検算を行う場合、1分という時間は非常に有効です。
例えば、2024年度の灘中学校で出題された以下の問題。

大問2　太郎君は1本の値段が□円のペンを5本買う予定でしたが、所持金が120円足りませんでした。
代わりに、1本の値段が予定していたものより100円安いペンを7本と60円の消しゴムを1個買ったところ、ちょうど所持金を使い切りました。

大問6　1、2、3、4、5、6、7、8から異なる4つを選び、大きい方から順にA、B、C、Dとしました。また、選ばなかった残りの4つを並び替え、E、F、G、Hとしました。すると、4桁の数ABCDから4桁の数DCBAを引いた差は4桁の数EFGHでした。4桁の数ABCDは□です。

大問2は差集め算、大問6は数の性質についての問題です。いずれも、解答を出すには少し時間を要します。（大問2の答え：260　大問6の答え：8532）
一方、それぞれの答えを確かめる場合は、
大問2…260×5－120＝1180　（260－100）×7＋60＝1180 より一致
大問6…8532－2358＝6174 より8つの数字が1回ずつ使われているので正しい
というシンプルな計算を行えば良く、慣れていれば1分程度で検算できます。
解いた後に検算をしない、という話は時折耳にしますが、上のように、大問1つの答えを1分で確実なものにできる、と考えれば、その重要性が見えてきます。
普段の学習や模擬試験の際にも、見直し・検算を欠かさずに行い、入試本番に備えておきましょう。

いかがでしたでしょうか。
「1」という数が持つ影響力は、様々な場面で大きく働きます。
その力を活かせるかどうかは、一日一日の学習の積み重ねで決まりますので、丁寧に学習するという意識を常に持ちましょう。

さて、冒頭で挙げたクッキーの例ですが、「チョコチップクッキー」という判定が出るクッキーには、以下の2パターンが存在します。
①本当にチョコチップクッキーで、正しく「チョコチップクッキー」と判定されたもの
チョコチップクッキーは100枚あり、その内の99%、すなわち99枚が正しく判定されるので、①のクッキーは99枚あります。
②本当はプレーンクッキーだが、誤って「チョコチップクッキー」と判定されたもの
プレーンクッキーは9900枚あり、その内の1%、すなわち99枚が誤って判定されるので、②のクッキーは99枚あります。
……なんと、①のクッキーと②のクッキーは共に99枚あることになりました。どちらも同じ枚数ですので、「チョコチップクッキー」と判定されたクッキーが実際にチョコチップクッキーである可能性は50%、すなわち五分五分となります。
「プレーンクッキー」の枚数が多くなればなるほど、②のクッキーの枚数も多くなっていき、「クッキーが全部で100万枚、そのうちチョコチップクッキーが100枚」という場合だと、取り出したクッキーが「誤って『チョコチップクッキー』と判定されたもの」である可能性は99.02%まで上がってしまいます。この場合、取り出したクッキーが本当にチョコチップクッキーである可能性はわずか0.98%ということになります。
勿論、これは「検査が不正確だ」という意味ではなく、母数（全体の数）が多くなれば、ほんの少しの誤差が大きな意味を持ってくる、ということを示しています。
成績の良い順に合格者が決定される中学入試では、「1点」の差、順位「1つ」の差がとても重要です。
持てる時間を「一分一秒」でも有効に活用し、「1つ」でも多く正確な解答を出して、合格へ「一歩」近付きましょう。

それでは、今回はこの辺りで失礼いたします。