こんにちは。頭を回転させるのが大好きな永田です。
いきなりですが、小学校の「算数」と中学校以降の「数学」の違いは何でしょうか。もちろん、どんどん複雑なものを扱うようになっていくというのもありますが、扱う内容が抽象的になっていくというのが大きな変化だと思います。例えば中学入試の問題であれば「〇〇さんが~求めなさい」となっているものが、数学だと「xの値を求めなさい」となっていきます。
もちろん、抽象的にすることで良いこともあります。今「つるかめ算」「倍数算」「消去算」などと別々のもののように扱っている問題は、中学に入ったら「連立方程式」という1つのものにまとまります。わざわざこの場合はこう解いて・・・などと考えず、式で表して同じように解いていくことができるようになります。中学受験の勉強でも、「マルイチ算」は少し抽象に寄った考え方ですね。
しかし、これまで具体的な問題を中心に考えてきたものを、突然抽象的にしろと言われても難しいもの。使いこなせれば大きな武器になりますが、そこまで行くのには時間がかかります。
そんな背景があってか、難関校の問題では時々やや抽象的な問題が出てきます。何だかわけのわからない操作が書いてあって、最初は指示に従っていけば解けるものの、後半の問題はどこから手をつけたらよいのかわからない、そんな問題です。
そういった問題にどのように対処すればよいか、その1つの手法が具体的な状況を想像することです。上手に問題文を翻訳してやって、聞かれている内容を具体化できれば、意外と簡単に解けるということがけっこうあります。百聞は一見にしかず、実際にどのように翻訳するかを見てみましょう。
では、例題として次の問題を考えてみてください。
[問] 記号【X、Y】は、XとYの大きな方から小さな方を引いたときの差を表すこととします。例えば【1、3】は3-1 = 2、【6、2】は6-2 = 4、【5、5】は5-5 = 0 となります。
サイコロを4回ふり、出た目を順にA、B、C、Dとします。このとき、【1、A】+【A、B】+【B、C】+【C、D】+【D、6】の値は、最も小さいときいくつになりますか。
いかがでしょうか。まずは何といってもこの式の形。約束記号をたくさん使って何を計算したいのかとても見づらくなっています。では手当たり次第に試していけるかというと全部で1296通りもあってそれも無理。さらに、「値が最も小さいとき」を求めないといけないので、いくつか試したと答えの見当をつけたとしても本当に一番小さい値を求められたのか?と不安になってしまいそうです。
では、この問題を翻訳していきましょう。
記号【X、Y】の意味をわかりやすくするために、右の図のような6つのマス目を考えて、サイコロの目と同じマスに移動すると考えてみましょう。すると、【X、Y】というのはXのマスからYのマスに移動するときに何マス移動したか、というのを計算していることになります。
では、【1、A】+【A、B】+【B、C】+【C、D】+【D、6】という式は何を表しているのか。最初の【1、A】というのは、はじめは①のマスにいたのが1回サイコロをふって何マス移動したかということになります。次の【A、B】は2回目にサイコロをふったときに何マス移動したか、・・・そして4回サイコロをふって移動したあとに【D、6】で⑥のマスに移動して何マス移動したか、と考えることができます。
この考え方を基に、先ほどの問題を翻訳すると次のようになります。
[問’] 左から順に①、②、③、④、⑤、⑥と並んだマス目があり、最初は①のマスにいます。1回サイコロをふるごとに、サイコロの目と同じマスに移動します。4回サイコロをふった後、最後に⑥のマスに移動するとしたとき、移動したマス数は一番少なくて何マスになりますか。
どうでしょうか。先ほどの問題よりはかなり状況がわかりやすくなったかと思います。
ここまで来てしまえば、あとは計算なしで解けます。最初は①にいて最後は⑥に行くのだから、ずっと右に進み続けるのが一番移動したマス数が少ない進み方になります。つまり、途中で何回か止まったとしても、6-1 = 5 が一番少ないマス数になります。
ちなみにこの問題の元ネタは何かというと、北海道大学の入試問題(2023)です。もちろん中学入試風に書きかえてはいるのですが、聞かれている内容はまったく同じです。大学入試の問題ですら、うまく翻訳すれば小学生でも手が届く問題になるのです。翻訳のパワーを感じていただけたでしょうか。
次は、中学入試の問題を翻訳してみましょう。早大学院の2022年の問題になります。
[問](抜粋)いくつかの〇が数をもつ線で結ばれた図を考えます。次の手順で、Sの〇からGの〇まで各〇に数を書き込み、数を確定させていきます。数が確定した〇には、目印として色をぬっていきます。
手順1 Sの〇に0を書き込む。
手順2 色がぬられていない〇のうち、最も小さい数が書かれた〇を1つ選び、数を確定させてその〇に色をぬる。
手順3 手順2で色をぬった●と直接結ばれた〇について、「●に書かれた数」と「●と〇を結ぶ線がもつ数」の合計を〇に書き込む。直接結ばれた〇が複数ある場合、すべての〇に同様に合計を書き込む。ただし、すでに〇に数が書かれている場合、書き込もうとする数がすでに書かれた数より小さいときは書きかえ、小さくないときは書き込まない。
手順4 Gの〇に色がぬられていれば終了し、そうでなければ手順2に戻る。
例えば、下の図1が与えられた場合、次のように数を確定していきます。
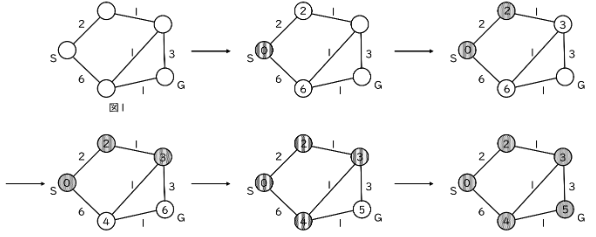
図2(略)において、上の手順を終えた後にGの〇に確定される数を求めなさい。
図3(略)において、上の手順を終えた後にGの〇に確定される数を求めなさい。
図3において、線を1つ取り除くことを考えます。
① Gの〇に確定される数が線を取り除く前と変わらないような線の取り除き方は何通りありますか。
② Gの〇に確定される数が最も大きくなるように線を取り除きます。取り除く線がもつ数と、Gの〇に確定される数を求めなさい。
このような問題になります。(1)と(2)については、図は複雑になりますが手順に従って計算していけば答えが出ます。しかし(3)については、この図と手順が何を表しているのか、裏に隠れたテーマに気付けないとどこから手をつけるか見えにくい問題です。
では、この問題を翻訳していきましょう。右の図1’は、先ほどの図1に説明のためA~Cの記号をつけたものです。この図を例えば次のように考えてみましょう。
S町、A町、B町、C町、G町があり、道が図1’のようにつながっています。町の間を移動するには、(道の横に書いてある数字)分だけかかります。例えば、S町とA町の間は2分、C町とG町の間は3分かかります。
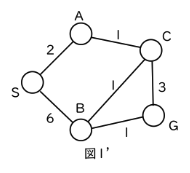
この考え方では、手順1~4は何を求めていることになるでしょうか。最初にAとBに入る2と6は、S町からA町やB町に行くとそれぞれ2分と6分かかり、次にCに入る3は、S町→A町→C町と移動すると合計3分かかることを示しています。
では、Bに確定した4は何になるでしょうか。S町→B町では6分かかりますが、S町→A町→C町→B町なら4分で移動できます。つまり、それぞれの〇に確定される数は、S町から最速で移動するときに何分かかるかということを表しているので、この問題は最速経路を探す手順を扱っていると見ることができます。図1’の場合、S町からG町へ最も速く移動しようとすると、S町→A町→C町→B町→G町と移動することになります。
このように翻訳してしまえば(3)の①は楽なもの。線を取り除く=通行止めと考えて、通行止めになっても最速経路に関係ない道を探せばよいのですから、通っていない道を選べばよいことになります。図1’の場合であればS町―B町間、C町―G町間の2通りが当てはまります。②はさらに丁寧に調べないといけない問題ではありますが、調べる候補を絞ることはできるはずです。
このように、具体的な状況を想像して、問題で聞かれているものが何を示しているのかをイメージすることができれば、見た目は難しい問題も意外と楽に解けることがあります。とは言っても、いきなり試験本番で想像してみろと言われてできるものではありません。ちょうどこれから受験生は過去問に触れる機会が多くなる時期。抽象的な問題に当たったら、どんな具体化ができるか考えてみるのも面白いのではないでしょうか。
それでは皆様、Have a good math.




