こんにちは。理屈家な講師の永田です。
とある日の夜のこと。帰宅途中に歩きながらある問題の解説方法を考えていたのですが、その途中でふと気になることがありました。
「あれ、この論理展開って・・・小学生相手に使って大丈夫かな・・・」
文章の組み立てには論理が必須なわけなのですが、小学校の間はしっかりと論理について学ぶことはありません。もちろん感覚的に身につけている部分はあると思いますが、基礎がしっかりしているほうが望ましいのは明らかでしょう。
ということで、今回から何回かに分けて、論理学の基礎を小学生向けに解説していこうと思います。初回となる今回は、必要な用語の解説と、論理学の基本となる4つの論理記号のうち3つについて説明していきます。
用語
1つだけ、日常ではまず出てこない用語を解説します。「命題」という言葉で、「正しいか誤りかが明確に決まる文章」のことを表します。その文章が正しいか誤りかは関係ありません。「6は2の倍数である」「セミは昆虫の仲間である」「日本の首都は大阪である」はすべて命題になります。
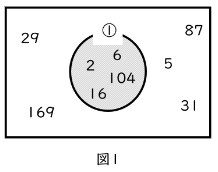
ここで、①「ある整数Aは偶数である」という文章を考えてみます。この文章のAに何か整数を入れると、正しいか誤りかが決まるようになるので命題になります。命題が正しくなるような数は図1の丸で囲った中に、誤りになる数は丸の外に書いていくようにすると、整数を2つにわけることができます。これが、①という文章の正誤を表すベン図になります。
以降の図では、正しい部分に色を着けて表すことにします。
*ベン図とは、「当てはまるものを線で囲った中に入れて表したもの」です。算数では数の性質や場合の数の単元ででてくるものですね。
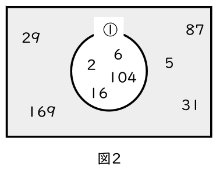
では、「①が誤りになる範囲」はどのように表せばよいでしょうか。もちろんこの場合は、丸の外にある数はすべて奇数なので、「ある整数Aは奇数である」という文章で表すことができます。
ただ、新しく文章を用意するよりも、既にあるものを使って表したほうが楽です。そこで1つ目の論理記号「not」が出てきます。notは「否定」を表す記号で、正誤を完全にひっくり返すはたらきがあります。「not ①」であれば、図2のように、丸の外が正しい部分になります。
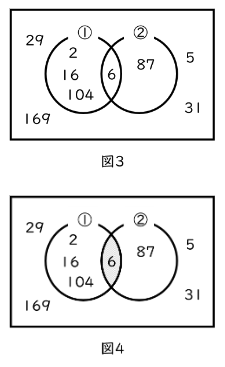
1つの文章で表せるのはここまで。これからは2つ目の文章が必要になります。ということで②「ある整数Aは3の倍数である」という文章を考えましょう。
①と②の文章を合わせて表すと図3のようになります。ようやく算数の問題で出てくるような図になりましたね。①と②の重なり方を考えるために、論理記号を2つ使います。
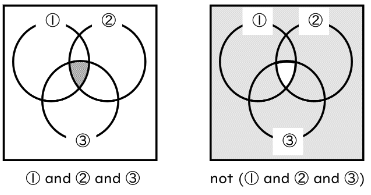
1つ目は「and」、難しくいうと「論理積」というもので、「andの前後の両方が正しいときだけ正しい」というものです。「① and ②」という文章を考えると、「ある整数Aは偶数である」と「ある整数Aは3の倍数である」が両方成り立たないといけないので、「ある整数Aは6の倍数である」と同じ意味になり、両方の丸が重なる部分だけが正しくなります。
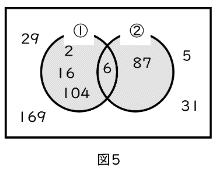
2つ目は「or」、こちらは「論理和」といい、「orの前後のどちらか片方でも正しければ正しい」というものです。「① or ②」という文章であれば、「ある整数Aは2か3で割り切れる」と同じ意味です。図で表すと、どちらかで色が着いている部分全体で図5のようになります。
ここで、両方の丸が重なる場所も正しい部分になっていることにご注目。「or」は「~または~」や「~か~」と訳されることが多いですが、論理学ではこの「または」に「どちらか片方」という意味はありません。ここは日常的な言葉とややずれる部分ですね。
これまでに出てきた3つの論理記号not、and、orに、優先順位を表す( )を組み合わせれば、ベン図の好きな部分を表現することができるようになります。試しに、下の問題に挑戦してみましょう。解答と解説は最後にあります。
問題
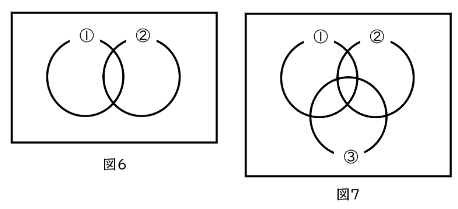
当てはまる部分を示しなさい。(1)~(3)は図6,(4)~(6)は図7です。
(1) (not ①) and ②
(2) not (① or ②)
(3) ① or (not ①)
(4) (① and ②) and (not ③)
(5) (① or ②) and ③
(6) not (① and ② and ③)
さて、ここまで論理学の基本部分を簡単に紹介してきたわけですが、お気づきでしょうか。ここまで論理学と言いながら、因果関係に関わるものがまったく含まれていないのです。論理学で因果関係を一手に引き受けるのが4つ目の論理記号「→」(ならば)なのですが、これだけはベン図で説明するのが難しいのです。ということで次回は、「→」の導入を兼ねてすべて表で処理する方法を紹介します。
それでは皆様、Have a good math.
解答
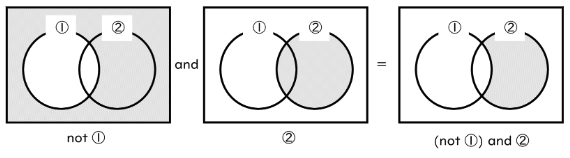
(1) (not ①) and ②
not ①と②をそれぞれ考えて、共通する部分を探しましょう。
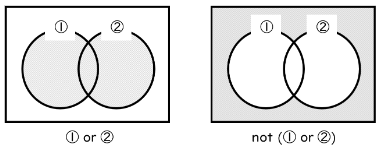
(2) not (① or ②)
最初に① or ②を考えた後で、notで全体をひっくり返します。
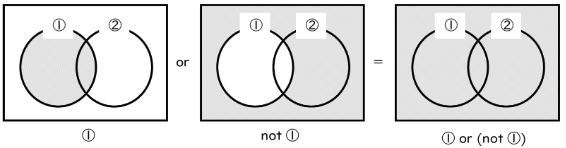
(3) ① or (not ①)
「①だろうが①じゃなかろうが」=①に関係なくなります。
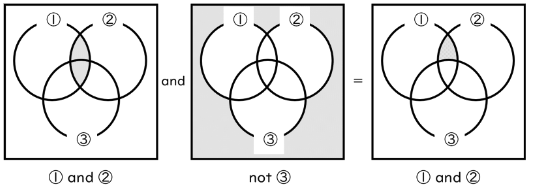
(4) (① and ②) and (not ③)
順番通りに処理していけば下のようになります。ちなみに、( ) の場所を変えて ① and (② and (not ③))としても同じ結果になります。
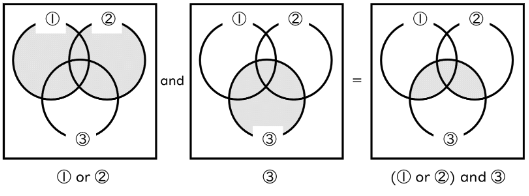
(5) (① or ②) and ③
これも順々に処理していくだけです。算数よりは理科ででてくるような形ですね。
(6) not (① and ② and ③)
( )の中を先に考えてnotでひっくり返します。言葉に直すと「『①でも②でも③でもある』ではない」です。「①でも②でも③でもない」を表したかったら「not (① or ② or ③)」とorを使います。