こんにちは。理屈家な講師の永田です。

前回の記事では、基本の論理記号４つのうち３つをベン図で説明しました。今回は、表を使った別な表し方を紹介しながら、４つめの論理記号「→」（ならば）について説明していきます。

最初に簡単な用語の復習から。論理学では「命題」という、正しいか誤りかがはっきりと決まる文章を扱います。前回も同じ例を出しましたが、「６は２の倍数である」「セミは昆虫の仲間である」「日本の首都は大阪である」という文章はそれぞれ正、正、誤と決まります。わざわざ漢字で書くのは大変なので、正は〇、誤は✕と表すことにしておきましょう。

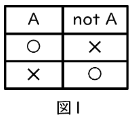
ではまず一番単純な「not」からいきましょう。notはその命題を否定するもので、上の3例にnotをつけると「６は２の倍数ではない」「セミは昆虫の仲間ではない」「日本の首都は大阪ではない」となります。それぞれ✕、✕、〇になりますね。このようにnotは、その命題の〇✕を入れかえるはたらきがあります。

表でまとめると図１のようになります。このように、与えられた命題（入力）に対して、その論理記号がどのような結果を与えるか（出力）を全ての場合についてまとめた表を真理値表といいます。

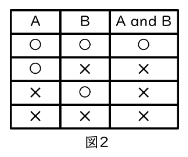
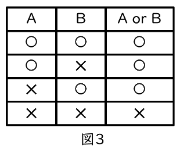
次に「and」と「or」をまとめて見ていきましょう。notの場合と違い、andとorは２つの命題が入力になるので、表が縦横に長くなります。A and Bの場合は、AとB両方とも〇な場合のみ〇、A or Bの場合は、AとBどちらかが〇なら〇になるので、それぞれ真理値表は図２、図３のようになります。

では今回の本題、「→」（ならば）について考えていきましょう。
まずは、「ならば（なら）」を使った文を具体的に考えてみましょう。例えば「次のテストで80点以上を取ったなら、ご褒美をあげる」みたいな文が考えられます。「ならば」という言葉は、前に条件、後にその条件が満たされたときの結果が入る接続詞であると言えます。
では、「次のテストで80点以上を取ったなら、ご褒美をあげる」という文がウソになるのはどのような場合でしょうか。それぞれ場合分けして考えてみましょう。
まず、80点以上取ったからご褒美をあげた場合。もちろんこの場合文は正しいです。
次に、80点以上取ったけどご褒美をあげなかった場合。これはあきらかにウソになりますね。

では、80点を取れなかった場合はどうなるでしょうか。「80点以上を取ったなら～」という文章では、80点を取れなかったときのことは何も言っていません。ですから、「80点取れなかったからご褒美はなし」としても、「80点は取れなかったけど、努力賞はあげる」としてもどちらもウソにはなりません。

以上のことをまとめてみると、「→」の真理値表は図４のようになると考えられます。実際これが「→」の真理値表になっています。これまでに出てきたandやorと比べて、AとBを入れかえると結果が変わるというのが大きな特徴ですね。

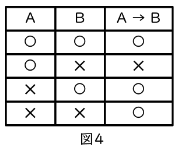
真理値表を使うと、例えば次のようなことがわかります。

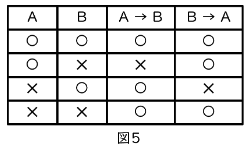
・A→Bであっても、B→Aとは限らない（図５、逆は必ずしも真ならず）
A→Bの真理値表とB→Aの真理値表は一致しません。「次のテストで80点以上を取ったなら、ご褒美をあげる」の例で、80点に届かなかったけど努力賞をもらったからといって、テストの点数が80点以上に修正されるわけではありませんね。

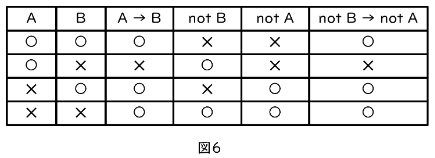
・（A→B）と（not B→not A）は同じ（図６、対偶）
この場合は真理値表が一致します。中学以降でよく見ることになります。同じ例で言うと、ウソをついたのでなければ、ご褒美がなかったのであればテストの点数は80点に届かなかったことになります。

・前提の間違った話は意味がない
前提（A）が×なら、結論（B）はどうなろうが理論自体は正しくなります。考え方は正しいのに変な結論になるのであれば前提を疑いましょう。

最後に、今回の内容を扱った入試問題があったので紹介したいと思います。茗溪学園2020年度の理科の問題です（抜粋・改題のうえ、表記をこの記事に合わせて変えてあります）。

問　この問題では、スイッチがオンなら〇、オフなら✕と表します。また、豆電球が光っているときは〇、光っていないときは✕と表します。
図７の電気回路では、スイッチがオフだと豆電球が光りますが、スイッチをオンにすると、下の導線の方に大きな電流が流れて、豆電球が光らなくなります。

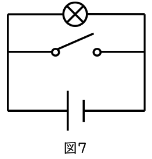
(1)スイッチを入力、豆電球を出力とすると、図７の電気回路はどの論理記号と同じことを表していますか。
(2)乾電池1個、豆電球１個、スイッチ2個を使って、論理記号「or」と同じことを表す電気回路を作りなさい。

(1)は表を作れば、(2)はどのような回路になればよいかを考えればできると思います。答えは下に書いておくのでぜひ考えてみてください。

前回と今回で基本的な論理記号４つをすべて知ったことになります。次回は、論理の実践的な使い方を、有名なパズルを題材に解説していきます。

それでは皆様、Have a good math.

答え

(1)not
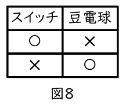
スイッチと豆電球の〇✕の関係は図８のようになります。notの真理値表と同じ結果になりますね。

(2)（例）図９
どちらか片方でもスイッチを入れれば豆電球が光るように、スイッチが並列に並んだ回路になっていれば大丈夫です。