こんにちは。理屈家な講師の永田です。
前回の記事では、真理値表を使って論理記号「→」(ならば)について説明しました。今回は、有名なパズルを使って、「→」の使い方に慣れていきましょう。
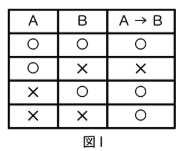
まずは「→」(ならば)の性質を復習しておきましょう。A→Bという記号を翻訳すると「A(である)ならばB(である)」となり、Aという条件を満たすならばBという結果になるということを表しています。「Aでない場合」については何も言及していないため、Aでない場合に結果がどうなってもかまいません。A→Bが間違いとなるのは、条件のAを満たしているにもかかわらず結果のBにならない場合だけです。図1の真理値表を確認しておきましょう。
では、今回扱うパズルを紹介します。
4枚のカード
すべてのカードには表面に赤か青の色が塗ってあり、裏面にひらがなかカタカナが1文字書かれている。今、机の上には4枚のカードがあり、下の図のように見えている。
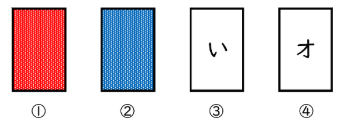
このとき、次の文章が正しいかどうか確かめるためには、少なくともどのカードをめくらなくてはいけないですか。
「赤いカードの裏にはカタカナが書かれている。」
問題自体は非常にシンプルですね。少し考えてみましょう。
~Thinking time~
答えは出せましたか?正解は①と③です。間違えるとしたら①と④という答えが多いのではないでしょうか。なぜ①と③になるか解説していきます。
まず、確かめたい文章「赤いカードの裏にはカタカナが書かれている。」を論理記号で書き換えてみましょう。
「赤いカードの裏にはカタカナが書かれている。」 = 「表の色が赤である」→「裏の文字はカタカナである」
この文章が正しいということは、A→Bが✕になることがないということ。つまり真理値表から、Aが〇でBが✕というカードがなければよいことになります。言葉に直すと「表の色が赤」であり、「裏の文字がカタカナでない」=「裏の文字がひらがな」であるカードがないことを示せば、文章の正しさが示せることになります。
では、1枚ずつめくる必要があるか確認していきましょう。
①表が赤なので、もちろんめくる必要があります。裏にカタカナが書いていないといけません。
②表が青なので、今回の文章にはまったく関係ありません。裏に何が書いてあろうが問題なし。
③裏にひらがなが書いてあるので、もし表の色が赤だったらあってはいけないカードになります。めくって表が青だといいですね。
④元の文章にカタカナという言葉が出てくるのでめくりたくなりますが、もし表が赤だったら文章に当てはまるカードになりますし、逆に表が青だったら条件にひっかからなくなります。どちらにしても文章の正しさにまったく影響しないため、このカードはほっておいて大丈夫です。
では、元の文章を次のように書き換えたらどうなるでしょうか?
(1)「表が赤でなければカタカナは書かれていない」
(2)『「赤いカードの裏にはカタカナが書かれている」かつ「カタカナのカードの表は赤である」』
(3)『「赤いカードの裏にはカタカナが書かれている」または「カタカナのカードの表は赤である」』
それぞれ、シンプルな形に書き換えたり、真理値表を考えたりしたうえで、どのカードをめくればよいか考えてみましょう。
以上、ここまで3回で、論理学の基礎に触れてみました。少しでも論理学を理解する助けになれば幸いです。
それでは皆様、Have a good math.
答え
(1)文章を書き換えると、「表が青である」→「裏はひらがなである」です。つまり確認するべきは「表が青で裏がカタカナのカードがない」ことなので、②と④をめくればよいです。
(2)真理値表を書いて考えましょう。「かつ(&)」なので、A→BとB→Aが両方〇でなくてはなりません。そのようになるのは「表が赤(A〇)で裏がカタカナ(B〇)」の組み合わせか、「表が青(A✕)で裏がひらがな(B✕)」の組み合わせだけです。つまり、表の色と裏の文字種が完全に1対1で対応していないといけないので、①、②、③、④のすべてのカードをめくって確認しなくてはいけません。
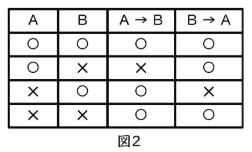
(3)今度は「または(or)」なので、A→BとB→Aのどちらかが〇であれば大丈夫です。A、Bがどのような組み合わせでも、A→BとB→Aのどちらも✕になることはないので、何も確認しなくてもこの文章は正しいといえます。おそらく直観的な答えとはずれると思います。
念のため、それぞれの色と文字の組み合わせについて確認しておきましょう。
①赤・カタカナ(A〇、B〇)のとき A→BもB→Aも正しい
②赤・ひらがな(A〇、B✕)のとき A→Bは誤り、B→Aは正しい orなので片方正しければok
③青・カタカナ(A✕、B〇)のとき A→Bは正しい、B→Aは誤り orなので片方正しければok
④青・ひらがな(A✕、B✕)のとき A→BもB→Aも正しい
よってどの色と文字の組み合わせでも(少なくとも論理学的には)元の文章は正しいことになります。




