今回のポイント　　　“１”変化させてみよう

 

【問　　題】
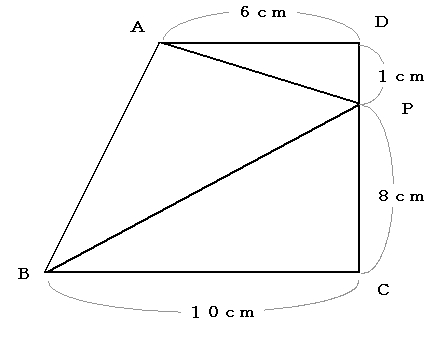
下図のような台形ＡＢＣＤがあります。Ｐは辺ＣＤ上の点です。
三角形ＡＢＰの面積が３０ｃｍ2のとき、ＣＰの長さは何ｃｍですか。

[桐朋2008年]

 

 

【解答・解説】

まず、皆さんが思いつく解き方は、三角形ＡＤＰと三角形ＢＣＰの合計の面積を
出すことです。

台形ＡＢＣＤ－三角形ＡＢＰ＝
（６＋１０）×９÷２　－　３０　＝７２－３０＝４２(cm2)

ここで“つるかめ算”で解く方法もありますが、
今回は違った方法で解いてみましょう。

 

　　　　～その１　極端な場合を考える～

 

極端な場合を考えてみましょう。点Ｐが点Ｄにあった場合、三角形ＡＢＰの面積は

６×９÷２＝２７(cm2)

では、点Ｐが点Ｃにあった場合、三角形ＡＢＰの面積は

１０×９÷２＝４５(cm2)

この２つから、三角形ＡＢＰの面積が３０cm2のときの点Ｐの位置は

点Ｄに近いことがわかります。

 

　　　　～“１”変化させてみよう～

 

点Ｐが点Ｄに近いのですから、点Ｄからどれだけ離れているかを出せば
いいことになります。

どれだけ離れているか、すぐにはわかりませんが、

とりあえず“１ｃｍ”動かした時、

三角形ＡＢＰの面積はどうなるか、を考えてみましょう。

 

 

三角形ＡＢＰ＝台形ＡＢＣＤ－(三角形ＡＤＰ＋三角形ＢＣＰ)

＝７２－(１×６÷２＋８×１０÷２)＝２９(cm2)

では、２ｃｍ動かしたらどうなるでしょうか。

三角形ＡＢＰ＝７２－(２×６÷２＋７×１０÷２)＝３１(cm2)

３ｃｍ動かすと

三角形ＡＢＰ＝７２－(３×６÷２＋６×１０÷２)＝３３(cm2)

三角形ＡＢＰの面積は点Ｐを点Ｄから点Ｃに１ｃｍずつ動かしてゆくと

０ｃｍ・・・２７ｃｍ2
１ｃｍ・・・２９ｃｍ2
２ｃｍ・・・３１ｃｍ2
３ｃｍ・・・３３ｃｍ2

つまり、１ｃｍ点Ｐを動かすと、三角形ＡＢＰの面積は２ｃｍ2ずつ
増えてゆくことがわかります。

３０ｃｍ2になるためには、３ｃｍ2増やせばいいので

３÷２＝１．５(cm)

点Ｐを点Ｄから点Ｃへ１．５ｃｍ動かせばいいことになります。
よってＣＰの長さは

９－１．５＝７．５ｃｍ

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　　７．５ｃｍ　　

 

　　　　～この解き方で麻布の問題も解けます～

 

【問　　題】

１辺の長さが１ｃｍの正六角形ＡＢＣＤＥＦがあります。
この正六角形の平行な２辺ＡＢとＥＤを同じ長さだけのばして、
図３のように新しい六角形を作ったところ、面積が二倍になりました。
この新しい六角形において、辺ＡＢの長さを求めなさい。

[麻布2012年]

 

【解答・解説】
下図のように正六角形ＡＢＣＤＥＦの面積は正三角形ＡＢＯの面積の６こ分です。

 

　　　　～１ｃｍのばしてみる～

辺ＡＢと辺ＥＤをとりあえず、１ｃｍ伸ばしてみましょう。
そうすると下図のようになり、正三角形ＡＢＯの面積の４こ分増えることが
分かります。

 

正六角形ＡＢＣＤＥＦの２倍の面積にすればいいのですから、
６こ分増やせばいいわけです。

６÷４＝１．５(ｃｍ)

６こ増やすには１．５ｃｍ伸ばせばいいので、辺ＡＢの長さは

１＋１．５＝２．５(ｃｍ)

 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　答　　　２．５ｃｍ　

 

この問題は2012年の麻布中学　問題６　(2)のアです。(2)のイ、(3)も
同じ解き方で解けますので挑戦してみてください。

問題を解くときにいきづまったら、とりあえず“１”変化させてみる！　です。