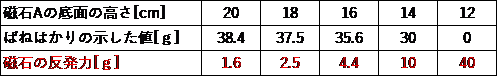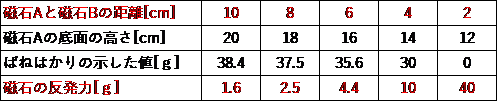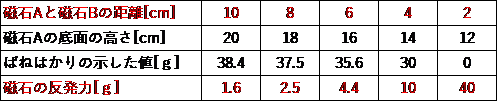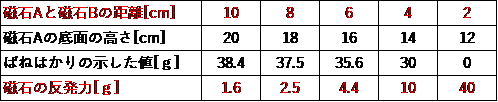今回は、前回の磁力①で紹介した入試問題の後半を解説します。
まずは問題の再確認から。
問題2(大宮開成中)
長さ10㎝、重さ40gの円柱状の磁石A、Bを用いて次のような実験を行いました。
【実験】
①図1のように、台はかり上にとう明なつつを置き、つつの重さが無視できるように台ばかりを調節した。台ばかりの測定台は磁石につかない素材でできているものを用いた。
②つつ内に磁石Bを立たせた。
③ばねばかりにつり下げた磁石Aをつつ内にそっと下ろし、台ばかりから磁石Aの底面の高さとばねばかりが示した値を測定した。測定は、ばねばかりが示す値が0gになるまでおこなった。そのときの磁Aの底面の高さは12㎝であった。
④結果を表にまとめた。

まず、文中の実験結果をまとめたこの表ですが、

問3の前に、この表にひと工夫加えますよ。
問2で考えたように、ばねばかりにかかる力が、磁石Aにかかる重力=40gからどれだけ軽くなっているかが、磁石に働く反発力になります。それを表に書き加えると、
↓こうなります。
さらに、磁石Aと磁石Bとの距離を書き加えてみると、
どうでしょう。このようにとらえることで、磁石の距離と力の関係がかなりつかみやすくなったと思いませんか。
なお、ここまでやると、磁石の距離が2倍、3倍、4倍、5倍に変化したとき、磁力の変化の仕方には明確な規則性があることがわかるのですが、発見できましたか。
距離が2倍、3倍、4倍、5倍になると、それに対応して、磁力は、
1/4倍、1/9倍、1/16倍、1/25倍に変化していますね。距離×距離に反比例しているのでした。
さて、本題に戻り、問3から考えていきますよ。
問3 磁石Aの底面の高さが14㎝のとき、台ばかりが示した値は何gですか。
先ほど作ったこの表から、反発力=10gのとき、台はかりにかかる力を求めればよいことがわかります。
この見えない反発力を見やすくするために、もう一工夫します。
反発力を表すもの、それは…
ばね。
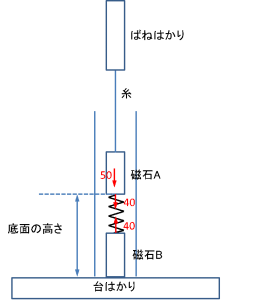
反発力を表すために、縮めたばねを書いてみると、こうなります。
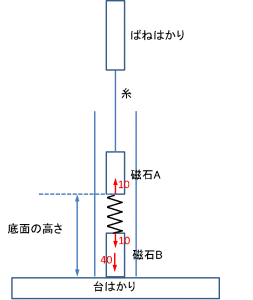
どうでしょう。磁石Bの重さは40gなので、この図より、台はかりにかかる力は
40+10=50g
であることがわかります。
それでは問4です。
問4 磁石Aの上下を実験の時と反対にして、同様の実験を行いました。磁石Aの底面の高さがある高さまで下がると、磁石Bが磁石Aに引き寄せられ、くっつきました。磁石Bが引き寄せられる直前の磁石Aの底面の高さは何㎝ですか。
「磁石Bが引き寄せられる直前の磁石Aの底面の高さ」とていねいに表現されています。
直前の状態とは、
重力=磁力(磁石の引き合う力)
の状態。すなわち
磁力=40g
の時です。これを少しでも超えて近づけると、
重力<磁力となり、磁石Bは磁石Aに吸い寄せられてくっつく、というわけです。
この「直前の状態」を表すために、問3と同様に、引き合う力を表す工夫をします。そうです。引き合う力を表すために、引き伸ばされたばねを書いて、力を記入していきます。
このようになります。こうすると、
引き合う力=40gということは、磁石の距離が
反発力=40gの時と同じになればよい(※)から、表より磁石の距離=2cmとわかります。
求めるのはこの時の「磁石Aの底面の高さ」ですから、
表より、12cmですね。
(※)のところは、やや荒っぽい推論になりますが、常識で予想することは十分できるでしょう。こうした対応力は、いろいろな問題を経験する中で身につけていきたいものです。知らないからといってあきらめず、経験から類推して乗り切ることを考えに入れて、対応力を高めましょう
今回の工夫のポイント
①表を分かりやすくするために、磁石Aの高さ→2つの磁石の距離
のように、新たに項目を作って、データを記入する。
データ読解を要する問題においては、こうした一手間は効率を大幅に高めてくれます。
②反発力、引き合う力をばねで表現する
目に見える、身近なばねを書き込むことで、力の働きが見えやすく、力を図示しやすくなりますね。
磁力を計算する問題はあまり多く出てきませんが、バネと同じということがわかってしまえば、覚えることは一つもありません!
これも力学の特徴と言えるでしょう。
それではまた。