前回に引き続き、対応で数える練習を行います。

父：前回のクイズの答え合わせからいくぞ。

良夫：③４勝かな。
父：残念。正解は、①２勝
なのだ。
良夫：えーっ。
父：たしかに一般的なトーナメント表だと、４勝か５勝しないと優勝できないんだけどな。サッカーに限ってはそうでもなくて、青森山田高校は、なんと４回戦から参加。初戦がいきなり準決勝ってことなんだ。
良夫：ほとんど将棋のタイトル戦みたいだなあ。名人に挑戦権獲得ってね。
父：そこまではいかないけどな。
今回は、次の問題を考えるぞ。

【問題】
下の図のように底面の半径が異なる円柱が６つあります。半径の小さな円柱の上に大きな円柱を乗せることはできません。底面の中心同士が重なるように次の円柱を乗せることにします。３つの円柱を使って立体を作る時、立体は何種類作れるか求めなさい。（頌栄女子学院）

父：どうだろう。
良夫：見当もつかないや。
父：じゃあとりあえず１個作ってみて。
良夫：これでどう？

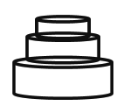
父：①中心が一致している　②小の上に大を乗せない。うむ、
指定通りに作れているな。
良夫：うん。
父：ほかに作れないか。
良夫：さすがに、これしかないでしょ。
父：そうか。じゃあ、最初に選ぶ３個の立体を決めれば、
良夫：自動的に１個に決まる。
父：では、３個の選び方は何通りあるだろうか。
良夫：チョーっと待った！３個の選び方だけ考えればいいってこと？
父：ばれちゃしょうがないな。
良夫：じゃあこの問題は
「６個の円柱から３個の円柱を選ぶ方法は何通りあるか」を
きかれているのと同じだね。それなら

で20通りと求められるね。
最初からそう言ってくれればチョー簡単じゃん。
父：それじゃあ面白くないだろ。
良夫：簡単すぎると差がつかないか。ところで、「底面の中心同士が重なるように」ってあったけど、こう考えていくとなんか正体を隠すための目くらましのような気がする。
父：どんな意図で作ったかは分からないが、不要な情報ではあるな。
この問題、もうちょっと言い換えられないか。そもそも円柱って必要だろうか。
良夫：うーん。
大きさの違う６個の立体だから、最初から数字の1,2,3,4,5,6でいい気がする。
父：よくぞ言った。
良夫：ということは、こうなるのか。
「数字の１から6の中から3つを選んで、小さい順に並べてできる3桁の数字は何個あるか」
父：これで完全に「対応で数える」ことに成功したな。
良夫：これなら楽だなあ。
父：ところでこの問題で
6種類の円柱が１個ずつでなく、それぞれ大量にあるとしたら、どうなる？
良夫：よし。「対応」で挑戦するぞ。
「１から６までの数字を使って、百の位＜十の位＜一の位となるような３桁の数字を何個作れるか」を考えればいいね。そのためには、
大きさの異なる３つの数を選べばいいよね。
父：その後は？
良夫：その後は…あれ、さっきと同じだ。大きさの異なる３つの数字は、自動的に１つの数字と対応する。だから、

で20通りになる。結局さっきと同じなんだ。
父：ああ。同じ数字がたくさんある時は、「異なる３つの数」を選ぶことがポイントということになるな。
良夫：表面的なことに振り回されずに問題を言い換えていけば、楽ができるってわけだ。
父：その、楽をしようとする気持ち…
良夫：えっ
父：楽をしようとする気持ちは、大切だ。
良夫：何それ。なんでそう思うの？
父：楽をするために工夫をするわけだから、自分から湧いてくる気持ちでないとこうはいかないんだよ。他人から押し付けることは不可能だからな。

まとめ

意識的にやると、別の場面でも使えることが出てきて役立つかもしれません。

冒頭のサッカー県予選についてのクイズですが、トーナメント表を初めて見たときは正直驚きました。一つ一つ勝ち進んだチームと争って、最後にシード校がおいしいところを持っていくような構図になっています。興味のある方はチェックしてください。

次回もお楽しみに。