「対応で数える」シリーズの第３回です。今回は図形の数え方を扱います。誰もが解いたことがある、中学受験の頻出問題です。

父：対応で数えることはわかってきたか。
良夫：そのまま数えるより、対応を使ってどんどん言い換えていくと、数えるのが楽なパターンが結構あることがわかった。
父：そうか。今回は図形問題だ。
良夫：と見せかけて、そうじゃないとか？（笑）
父：まあまあ、まずは問題をご覧ください。

問題

図のように、円周上に８等分する点を打ちます。この８個の点のうち３個を結んでできる三角形を考えます。
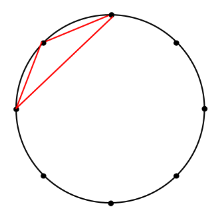
三角形の形は何種類作ることができるでしょうか。
ただし、回転したり、裏返したりしたものは同じ図形と考えます。

図2

図3

図4

図5

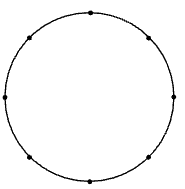
良夫：なんか大量にできそうな感じがするな。
父：じゃあ、何か1つ書いてみようか。
良夫：うん。

とりあえず、書いてみた。
父：ＯＫ。
良夫：これで１種類か。この調子で書き込んでいったら、すっごーい図になってしまいそうです。
父：はっはっは。そりゃそうだ。
良夫：ってことはここで何かに対応させることができると。
父：いい読みだ。
んじゃあ、3つの辺の外側に、数字を書き込んでみようか。
良夫：数字？
父:ああ。45度の弧を何個使っているかわかるだろう。
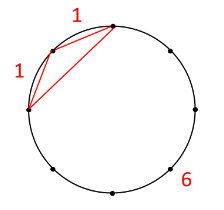
良夫：ああ、弧ね。1個、1個、６個だから、こうなる。
書いたよ。

父：ああ。そしたら、３つの数字に意識を集中してみてごらん。
良夫：じーっ…
何も起こりませんが。
父：数字に意識を集中すると、三角形が消えるんだよ。
良夫：どういうこと？
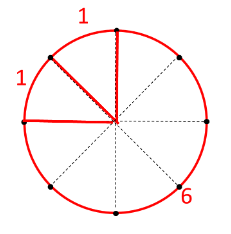
父：まず、おうぎ形に意識を向けるために、中心から半径を書いて、８つのおうぎ形に分けてみよう。
良夫：こうかな？

父：いいぞ。
ここでだ、意識をおうぎ形に向けるとどうなる。
良夫：おうぎ形に集中する。つまり、三角形を意識から外してこう見ろと？

父：ええでええで。
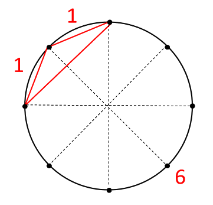
良夫：なるほどなあ。ってことは、８つのおうぎ型を３つに分割するってことになるな。
…あれっ？！
父：どうした？
良夫：扇形が消えた。
父：何と？！
良夫：図形が消えて、
父：図形が消えて？
良夫：8=1+1+6　だけが残った。
父：その心は？
良夫：８つのおうぎ形を３つに分割するってことは
8を3つの数の和で表すことと同じだね。
父：もはや三角形でもおうぎ形でもなくなっている！
良夫：ほらあ、だから最初に見せかけだけの図形じゃないのって言ったじゃないか。「図形の問題」って強調するから、怪しいと思ったんだ。
父：まあ、この問題で三角形を書き出すのはどう見てもうまくないからな。
良夫：こういう時こそ「対応」の出番だよね。なんか思考のパターンがつかめてきた気がする。
父：今回は最初から手を読まれていたようだな。それでも自力でここまでたどり着いたわけだから…
良夫：どれだけ楽したいんだ、ってことだね（笑）。

今回の「対応」

問題の答え:
8の分け方は以下のようになります。
(1,1,6)
(1,2,5)
(1,3,4)
(2,2,4)
(2,3,３)
答えは5通りでした。

これなら図形に翻弄されずに済みますね。
これらの小ネタは、単独で覚えるだけでもスピードアップに役立つネタであるのはもちろん、考え方そのものも応用することができるので、「楽したい気持ち」をもって臨めば、難しい問題もチャンスが広がるでしょう。
次回もお楽しみに。