「どれにしようかな」「運命の分かれ道」
これを表す強力な道具が、樹形図です。

樹形図を利用して全ての場合を丁寧に調べれば、必ず正解にたどり着けることを確かめていきます。

父：今回は樹形図の訓練を行う。まずは問題を見てくれ。

良夫：１，２，３，４，５の数字を並べる。その時の条件が
１番目に１は来ない
２番目に２は来ない
３番目に３は来ない
４番目に４は来ない
５番目に５は来ない
…こんな感じでいいかな？

父：そんな感じでいい。

（せっせと樹形図を書く）

順番と数字が一致しないものを書き出していくよ。
まず１番目に２が来る場合を考えるぞ。

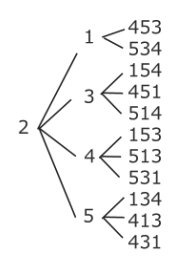
で、11通りある。
父：うむ。

良夫：あと、１番目が3,4,5のものも書き出すと…
それぞれ11通りあった。
だから、11×4＝44通り。

父：大正解！
さて、ここからが反省会だ。

良夫：トホホ。

父：44個書くのは大変だったか。

良夫：何をするかわかっているなら、大変ではないよ。でも、何をするのかがすぐに見えない場合は、つらい。あと、順番と数字が同じにならないように気を付けながらやるのは疲れる。

父：もっともだな。この問題で、省力化できそうなところはあるか。

良夫：そうだなあ。
1番目が2,3,4,5となる数の並びが各11個だったので、これは全部やらなくてもよさそうだ。

父：そうだな。

良夫：2,3,4,5は平等な感じがする。
あと、２番目の数字だけど、１を入れたとき（２個）と、それ以外のところ（３個）で結果が違っている。

父：3,4,5は平等だが、1はそうではないと。

良夫：そう思う。ここは不安だから、とりあえず11個全部書きだす、の方が安心だなあ。

父：自分にとって安心感があり、なおかつ無駄も少ない方法ということか。ベストに近づいてきたな。
あとは、最初に言ってた、何をやるかすぐ読み取れるかってところだが、

良夫：それはさすがに大丈夫。本当に５円玉って曲があるのか、と突っ込みたくはなったよ（笑）。

父：実は、この問題は、「完全順列」と呼ばれる有名数列を扱っているんだ。

良夫：へえ。

父：すべての数がもとの順番と違う位置に並ぶ方法が何通りかを表すのが完全数列なんだ。これって学校の席替えに似ていないか。

良夫：席替え？数字が順番の数と異なるということは、元の位置から移動したということか。じゃあ、
「全員の席が移動する方法は何通りあるか」、って感じかな？

父：そうだな、で、だから今回はこれを「席替え数」と呼ぶことにする。つまり…

良夫：全員の席が元の位置から移動する席替え方法を人数ごとに調べようってわけだね。

 

父：ああ。じゃあ１人からスタートする。
１人の席替え数を「席替え数1」と呼ぶ。席替え数１はいくつになる？

良夫：ええっ、動けないでしょ。

父：そう。だから席替え数１は、0通り。じゃあ席替え数2は？

良夫：さっきの数字で言うと、21の1通り。

父:正解。続けるぞ
席替え数3は？

良夫：
231
312
の2通り。

父：うむ。ここまでの結果をまとめるぞ。
席替え数１＝０
席替え数２＝１
席替え数３＝２
席替え数４＝９
席替え数５=44
ここまで調べたな。
「完全順列」は三角数なんかと同じ、有名な数列だから…

良夫：席替え数を覚えれば即使えると。しめしめ。いいこと聞いた。

父：ま、そういうことだ。

良夫：ところで席替え数６は？

父：急に大きくなるんだ。覚える必要はないかな…

良夫：ひょっとして、265になる？

父：ええっ。

良夫：なんとなくだけど…
こんな式が見えてきたんだ。

父：席替え数６も
（９+44）✕５=265で合ってる！すごいじゃないか。

良夫：合ってたんだ！数が並んでいると、なんかおいしい法則ないかなって探す癖がついちゃってて（笑）

父：なんという習性。ここぞというところで役立つといいな。

 

今回のまとめ

いかがでしたか。
過去問演習中に、「席替え数」を見つけたら、この結果が使えることを確かめてみてください。もちろん樹形図で「普通に」解いてもOK。
記述問題では使えないのでご注意を。

次回をお楽しみに。