みなさん、こんにちは。
受験ドクターの坂井です。
今回は完全シャッフルのお話です。
トランプでジョーカーを除く52枚のカードを上下の2つに分けてそれらを1枚ずつ交互に重ねて組み替えるという、トランプを切るときのお話です。
例えば8枚のカードに上から1,2,3,・・・、7,8と番号をつけてシャッフルを行うと
まず、1~4までのカードの束と5~8までのカードの束に分かれます。それを1枚ずつ交互に重ねて組み替えていくと、上から1,5,2,6,3,7,4,8 の順になります。
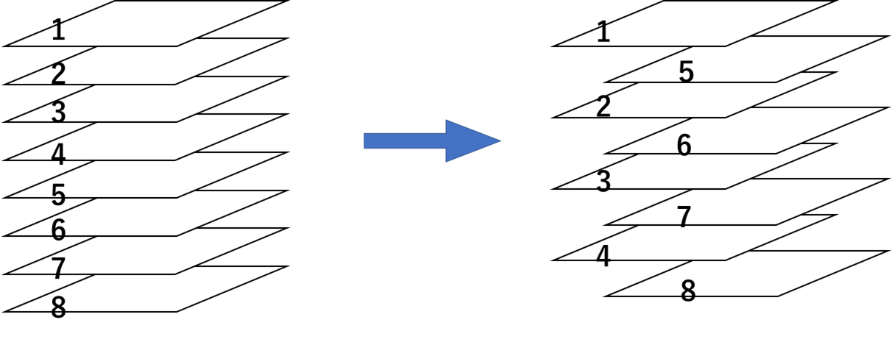
ここでそれぞれのカードの動きについて考えていきます。
一番上の1のカードと一番下の8のカードは動かず位置が変わりません。
上半分にある1以外の2~4のカードについては、上から2番目の2は上から3枚目に移動。上から3枚目の3は上から5枚目に移動。上から4枚目の4は上から7枚目に移動します。
つまり、1を除く上半分のカードについて、上からn番目のカードは(n×2-1)番目に移動していることがわかります。
下半分にある8以外の5~7のカードについては、下半分の上から1番目の5は上から2枚目に移動。下半分の上から2枚目の6は上から4枚目に移動。下半分の上から3枚目の7は上から6枚目に移動します。つまり、下半分の上からm番目のカードは(m×2)番目に移動していることがわかります。
これらをまとめると次のようになります。

これらのカードの動きに着目して
次の問題にチャレンジしてみてください。
おもてに1~52までの番号が書かれたカードがあります。これらのカードを上半分と下半分の26枚ずつの束に分けて、それぞれの束から交互に1枚ずつ取って重ねていき、図のように新しい束を作ります。これを操作1回とします。
(1) 2回の操作を行ったとき、上から9枚目のカードは上から何枚目になりますか。
(2) この操作を何回か行った後、上から9枚目のカードは再び最初の位置(上から9枚目)に戻りました。何回操作を行いましたか。
(1)上から9番目のカードは上半分のカードだから1回目の操作がおわったとき、
9×2-1=17番目に移動している。上から17枚目のカードも上半分のカードだから
2回目の操作がおわったとき、17×2-1=33枚目
33枚目
(2)(1)に続いて操作を繰り返していきます。
3回目の操作を行ってみます。33枚目は下半分の上から7枚目になるので
7×2=14枚目に移動します。
4回目の操作を行ってみます。14枚目は上半分の上から14枚目になるので
14×2-1=27枚目に移動します。
5回目の操作を行ってみます。27枚目は下半分の1枚目になるので
1×2=2枚目に移動します。
6回目の操作を行ってみます。2枚目は上半分の2枚目になるので
2×2-1=3枚目に移動します。
7回目の操作を行ってみます。3枚目は上半分の3枚目になるので
3×2-1=5枚目に移動します。
8回目の操作を行ってみます。5枚目は上半分の5枚目になるので
5×2-1=9枚目に移動します。
これではじめの位置に戻ってきました。 8回
ちなみに、上から18枚目と35枚目のカードは、なんと2回の操作でそれぞれもとの位置に戻ります。面白いですよね。この2枚のカードに何となく愛着を感じてしまいます。
以上、完全シャッフルのお話でした。




