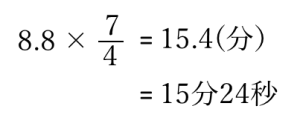みなさん、こんにちは。
受験Dｒ．の坂井智則です。
速さの問題を解くときは、通常、状況図やダイヤグラムをかいて整理しながら解いていきます。
隔たりグラフの問題も同様です。一見グラフがはじめから問題文で図示されているので、問題文に書いてある隔たりグラフに情報を書き込んで解こうとしてしまいがちなのですが、それは避けたほうが良いでしょう。より状況を正確に把握するために使い慣れた図で解いた方が確実です。
そこで今回のテーマがこれ。「ダイヤグラムにかき直してみよう」です。
問題文から2者の動きを読み取り、ダイヤグラムをかいてから解いてみましょう。
【問題】
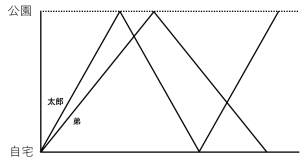
芝太郎君は弟と2人で自宅と公園の間を走って何度か往復します。
芝太郎君は弟よりも走るのが速く、2人は一定の速さで走ります。
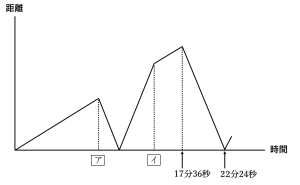
グラフは自宅から同時に出発した後の2人のへだたり（距離）と時間の様子を表しています。
(1) ア は 分 秒です。
(2) イ は 分 秒です。
（芝中）
【考え方】
問題文で 「太郎君と弟が自宅と公園の間を何度か往復する」といっているのでそのような動きのダイヤグラムをかいてみます。
(ⅰ) 太郎君が弟より早いので先に公園に着く。
(ⅱ) ２人とも公園までの行きと帰りの傾きが同
じになるようにする。
(ⅰ)（ⅱ）に注意しながらダイヤグラムをかくと右図のようになります。
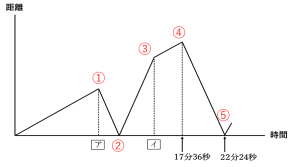
次に、かき出したダイヤグラムと問題文の隔たりグラフの①～⑤がどこで一致するのか照らし合わせてみます。
≪グラフからわかること≫
① 太郎君と弟の距離がだんだん離れていく。（太郎君が公園に着くまで）
② 太郎君の進む向きが変わり２人の距離がいっきに縮む
（２人の距離が0ｍのとき２人はすれ違う）
③ すれ違った後も２人は反対方向に進んでいるので２人の距離が大きくなっていく
（弟が公園に着く）
④ ③のときの２人の距離の差が少しずつさらに大きくなる（太郎が自宅に戻る）
⑤ ④で太郎君の進む向きが変わるので２人の距離がいっきに縮む
（２人の距離が0ｍのとき２人はすれ違う）
(１) ２人が同時に自宅を出発してから①までの時間と、②から④までの時間で、太郎君が進んだ距離が等しいので、 アは １７分３６分 ÷ 2 ＝ ８分48秒
8分48秒
(２)２人が同時に自宅を出発してから②<までの時間と②<から⑤<までの時間で、２人が進んだ距離の合計はそれぞれ自宅から公園までの道のり２本分で等しいので
②<の時間は出発してから ２２分２４秒 ÷ 2 ＝１１分１２秒後 であることがわかります。
そして２人がすれ違ったのは太郎君が公園を折り返してから２分２４秒後ということになります。
このことから下図のように、太郎君と弟の速さの比は 14：8 ＝ 7 : 4ということがわかります。
③は弟が公園についた時間なので、
15分24秒
今回は隔たりグラフをいったんダイヤグラムにかき出してから解いてみました。
状況図を用いて解いてもよいです。ただし問題文の隔たりグラフに情報を書き込み、状況図やダイヤグラムをかかずにそのまま解くことはお勧めしません。
必ず状況図やダイヤグラムにかき直してから解いてください。
特にダイヤグラムの利用は全体の状況が見やすかったり、問題によっては相似形を用いて容易に解答までたどり着けるといったメリットを持つ手法です。
ぜひ、チャレンジしてみてください。
それでは、またお会いしましょう。
