みなさん、こんにちは。
受験Dr.の坂井です。

通過算でもっとも重要な解法ツールは何だか知っていますか。
それは、何といっても作図です。
解き慣れてくると通過算の一行問題くらいは、いきなり式をかいて解くことができるかもしれませんが
少しでも問題が複雑になってくると作図をかかないで解くことはかなり難しいでしょう。

5年生のうちにマスターしておきたい通過算の作図を皆さんと一緒に考えてみたいと思います。

問題を解く際にマスターしておかなければいけない作図は次の通りです。

①電車が人の前を通過する図
②電車がトンネルを通過し終わる図
③電車がトンネルに完全に隠れている図
④貨物列車と急行列車がすれ違う図
⑤急行列車が貨物列車を追い越す図

それでは①～⑤がどんな作図になるのかを見ていきましょう。

【電車が人の前を通過する】（図１）

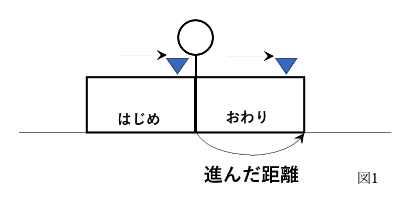
電車の先頭が人にさしかかった「はじめ」の電車の図と電車の最後尾が人にさしかかった「おわり」の電車の図をかきます。
重要なのは、電車が人の前を通過し始めてから通過しおわるまでに進んだ距離が
「電車の先頭から電車の先頭 」>であり、電車の長さと等しくなっているということです。

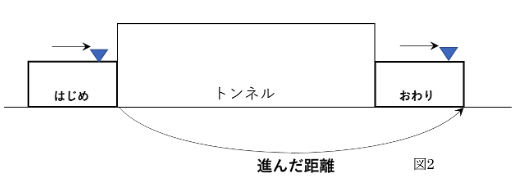
②【電車がトンネルを通過し終わる図】（図２）

電車の先頭がトンネルにさしかかった「はじめ」の電車の図と電車の最後尾が
トンネルの出口に重なった図をかきます。
重要なのは、電車がトンネルの前を通過し始めてからトンネルを通過しおわるまでに進んだ距離が
「電車の先頭から電車の先頭」であり、「トンネル＋電車の長さ」と等しくなっているということです。

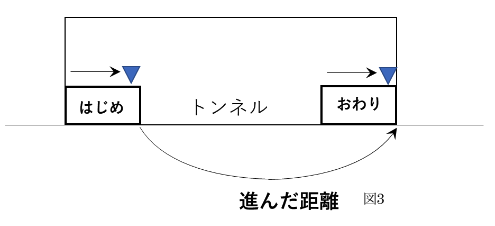
③【電車がトンネルに完全に隠れている図】（図３）

電車の最後尾がトンネルの入り口に重なる「はじめ」の電車の図と電車の先頭がトンネルの出口に重なった図をかきます。
重要なのは、電車がトンネルに完全に隠れている間に電車が進んだ距離は
「電車の先頭から電車の先頭」であり、「トンネル－電車の長さ」と等しくなっているということです。

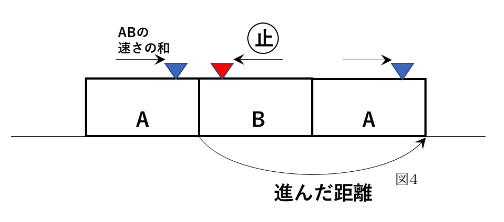
④【貨物列車と急行列車がすれ違う図】（図４）

電車Aと電車Bの先頭が重なった「すれちがい始め」と、電車Aと電車Bの最後尾が重なった「すれちがいおわり」をあわせた図をかきます。
電車が2つ登場してきますが、片方の電車（電車B）を止めて、その分もう片方の電車（電車A）が2つの電車の速さの和で動いていると考えます。
重要なのは、片方の電車を止めて考えるということと、すれちがい始めからすれちがいおわりまでの間に２つの電車の速さの和で進んだ電車Aの距離は、「電車Aの先頭から電車Aの先頭」であり、2つの電車の長さの合計と等しいということです。

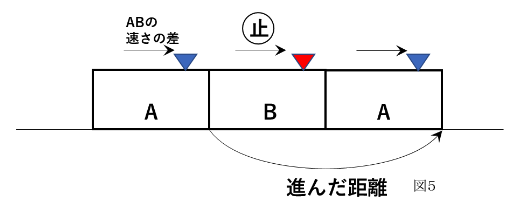
⑤【急行列車が貨物列車を追い越す図】（図５）

電車Bの最後尾と電車Aの先頭が重なった「追い越し始め」と電車Bの先頭と電車Aの最後尾が重なった「追い越しおわり」をあわせた図をかきます。④と同様に２つの電車が登場してきますが、追いこされる電車（電車B）を止めて追い越す電車（電車A）が２つの電車の速さの差で動いていると考えます。
重要なのは、追いこされる電車を止めて考えるということと、追いこし始めから追いこしおわりまでの間に２つの電車の速さの差で動いた電車Aの距離は、「電車Aの先頭から電車Aの先頭」であり、2つの電車の長さの合計と等しいということです。

通過算でマスターしなければならない５つの作図を見てきましたが、５年生は冬期講習期間で完璧に何も見ないでかけるようにすることを目指してください。

次回はこれらの作図を用いて、実際に問題を解いてみることにします。

それではまた、お会いしましょう。