みなさん、こんにちは。
受験Dr.の坂井です。
前回は通過算を解くうえで必要な5つの作図についてお話しました。
今回はそれらを利用してどのように問題を解くかを考えていきましょう。
【問題】
長さ120mの急行列車が人のまえを通過するのに5秒かかりました。
また、この急行列車がトンネルに完全に隠れている時間は12秒でした。
トンネルの長さを求めなさい。
5つの作図のうち。次の2つの作図を利用します。
2つの作図の重要なポイントについて再度確認してみましょう。
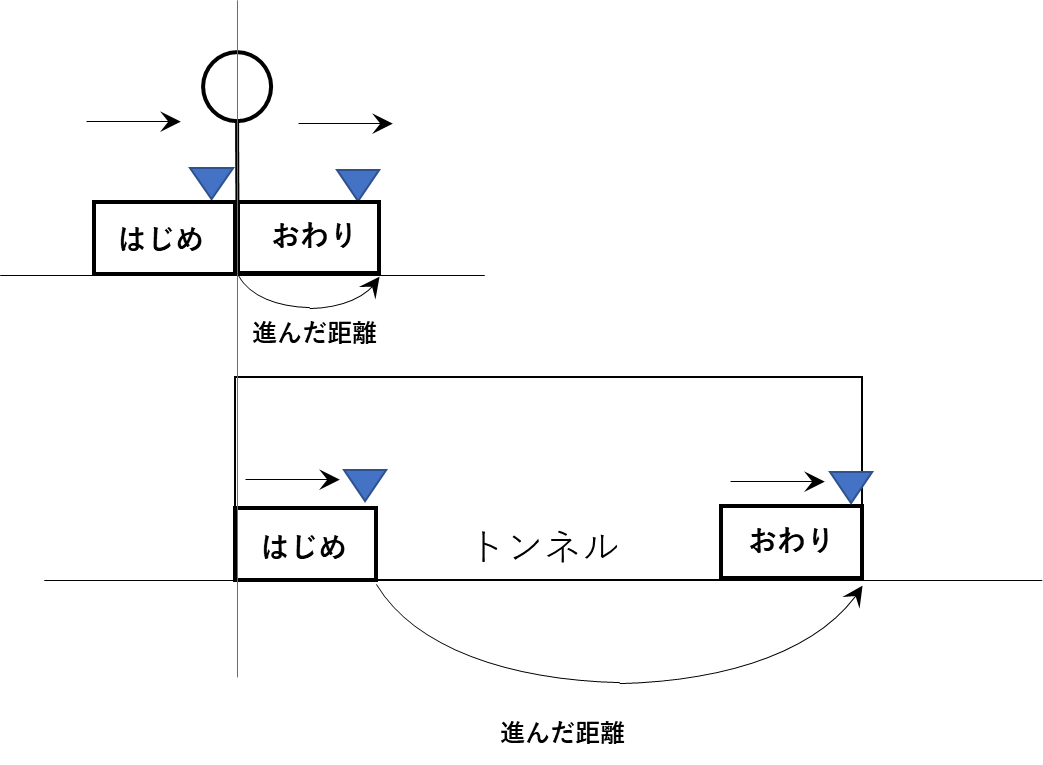
【電車が人の前を通過する図】
重要なのは、電車が人の前を通過し始めてから通過しおわるまでに進んだ距離が
「電車の先頭から電車の先頭 」であり、電車の長さと等しくなっているということです。
【電車がトンネルに完全に隠れている図】
重要なのは、電車がトンネルに完全に隠れている間に電車が進んだ距離は
「電車の先頭から電車の先頭 」であり、「トンネル-電車の長さ」と等しくなっているということです。
これらの2つの図を次のように重ねてみます。
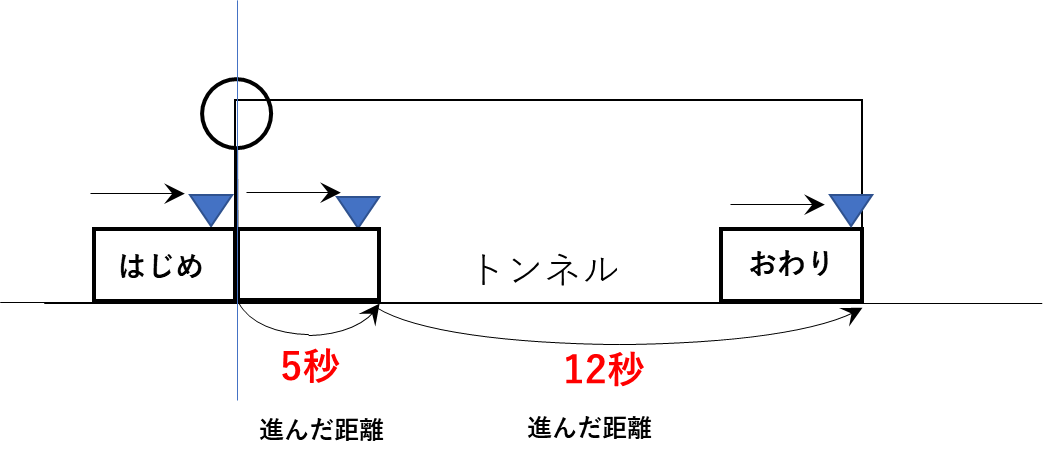
さらに、上段の人の前を通過しおわった「おわり」の列車を下段のトンネルに完全に隠れた「はじめ」の列車に重ねて作図すると次のような図になります。
すると、状況がはっきり見えてきました。列車の先頭がトンネルに差し掛かってからトンネルの最後の位置に到着するまでに 5+12=17秒 かかっていることがわかります。
また、列車の長さの120m進むのに5秒かかるので、列車の速さは秒速24mです。
よってトンネルの長さは 24m/秒 × 17秒 =408m となります。
通過算の問題は、いきなり式をかいて解き始めるケースはほとんどありません。
状況を把握してから解き始めることがセオリーです。その状況を把握するのに必要なものが作図です。
通過算を学習した5年生は必ず作図を意識して問題演習を行ってください。
【トレーニング】
秒速20mで走る貨物列車が長さ300mの鉄橋を渡りはじめてから通過しおわるまで21秒かかりました。
また、この貨物列車がトンネルに完全に隠れている時間は12秒でした。
トンネルの長さを求めなさい。
次の2つの図を利用します。
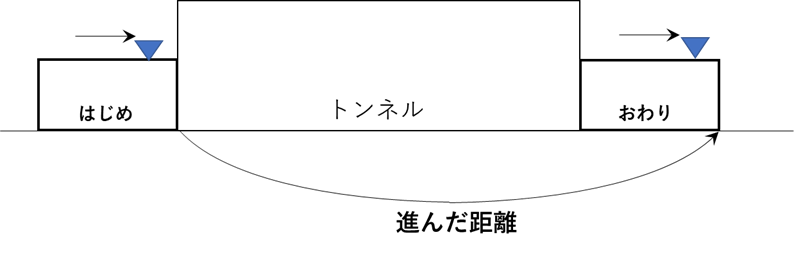
【電車がトンネルを通過し終わる図】
電車の先頭がトンネルにさしかかった「はじめ」の電車の図と電車の最後尾が
トンネルの出口に重なった図をかきます。
重要なのは、電車がトンネルの前を通過し始めてからトンネルを通過しおわるまでに進んだ距離が
「電車の先頭から電車の先頭 」であり、「トンネル+電車の長さ」と等しくなっているということです。
【電車がトンネルに完全に隠れている図】
重要なのは、電車がトンネルに完全に隠れている間に電車が進んだ距離は
「電車の先頭から電車の先頭 」であり、「トンネル-電車の長さ」と等しくなっているということです。
これらの2つの図を次ように重ねてみます。
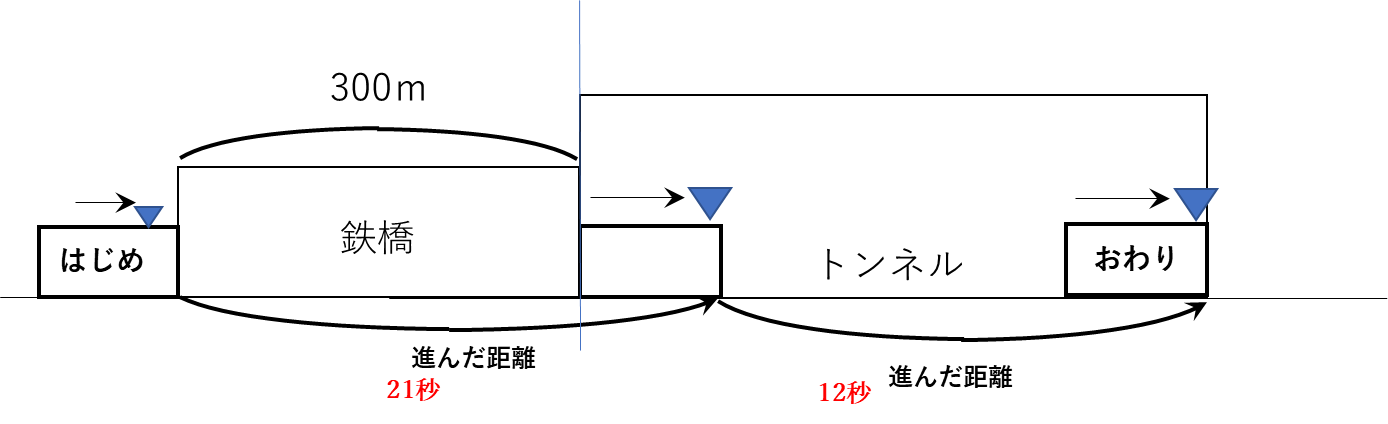
さらに、上段の鉄橋を通過しおわった「おわり」の列車を下段のトンネルに完全に隠れた「はじめ」の列車に重ねて作図すると次のような図になります。
すると、貨物列車の先頭が鉄橋に差し掛かってからトンネルの最後の位置に到着するまでに
21+12=33秒 かかっていることがわかります。列車の速さは秒速20mですから
鉄橋とトンネルの長さの合計は 20m/秒 × 33秒 =660m となります。
よってトンネルの長さは、 660-300=360m
それでは、みなさん
またお会いしましょう。