みなさん、こんにちは。
受験Dr.の坂井です。
今回は「数の性質」からのお話です。
そして問題を解決する方法として面積図を利用してみようという内容です。
では、問題。
【問題】 2022海城中
整数AをB個かけ合わせた数をA^Bと表すことにします。
例えば、7^2=7×7=49、
7^4=7×7×7×7=2401 です。
次の問いに答えなさい。
(1)7^8の千の位,百の位,十の位,一の位の数をそれぞれ求めなさい。
(2)7^20の千の位,百の位,十の位,一の位の数をそれぞれ求めなさい。
(3)7^100の千の位,百の位,十の位,一の位の数をそれぞれ求めなさい。
(1)解法として、がんばって7を8回かけてもよいでしょう。ちょっと大変ですが、気合と根性で正解までたどり着くことはできるでしょう。
7×7×7×7×7×7×7×7=5764801
ということで求める各位の数は 千の位⇒4 百の位⇒8 十の位⇒0 一の位⇒1
となります。
また、力わざで計算していくにしても、少し工夫して解くこと気づいた受験生を多いはず。
問題文中に7×7×7×7=2401と計算してくれているのでこれを利用することに気が付くことは容易です。
7^8=(7×7×7×7)×(7×7×7×7)=2401×2401 を筆算して下4けたのみ
計算すれば簡単にとけてしまいます。
では、これをあえて面積図を利用して考えてみましょう。
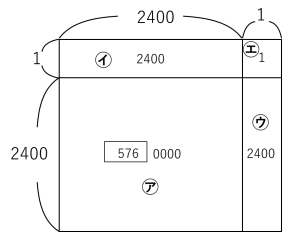
7^8=2401×2401 を面積図で表すと次の図のようになります。
この図を㋐,㋑,㋒,㋓のように4つの部分に分けてみましょう。
㋐の部分は 0000 となっているため、2401×2401の答えの下4けたの数は㋑+㋒+㋓の答
えと同じになります。
2400+2400+1=4801
つまり7^8の下4けたの数は、千の位⇒4,百の位⇒8,十の位⇒0,一の位⇒1であるとわかります。
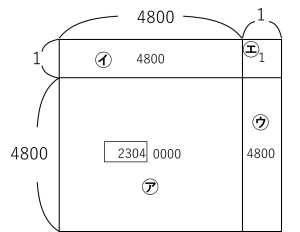
まず、(7^8)×(7^8)の答えの下4けたを考えてみましょう。
㋐の部分の下4けたは0000であるので、4801×4801の答えの下4けたの数は
㋑+㋒+㋓の答えと同じになります。
4800+4800+1=9601
つまり(7^8)×(7^8)=7^16の下4けたの数は、千の位⇒9,百の位⇒6,十の位⇒0,一の位⇒1であるとわかります。
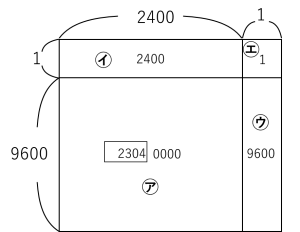
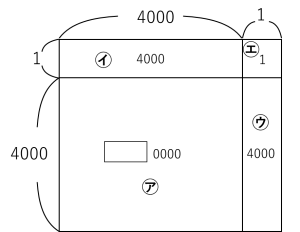
さらに7^20=(7^16)×(7^4)だから、下の面積図より、下4けたの数は
2400+9600+1=12001 となることがわかります。
千の位⇒2,百の位⇒0,十の位⇒0
一の位⇒0
(3)7^100=(7^20)×(7^20)×(7^20)×(7^20)×(7^20)
=(7^40)×(7^40)×(7^20)
=(7^80)×(7^20) と考えることができます。
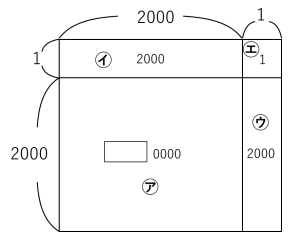
まず、7^40の答えの下4けたの数を考えてみましょう。
7^20の下4けたの数が2001だから下の面積図のようになります。
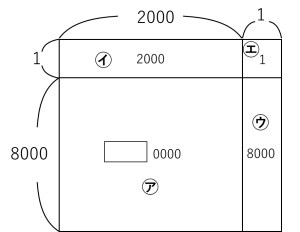
7^100=(7^80)×(7^20)だから
右の面積図のとおり、下4けたの数は
2000+8000+1=10001 となります。よって、7^100の答えは、
千の位⇒0,百の位⇒0,十の位⇒0
一の位⇒1 となります。
「数の性質」の分野の問題を面積図を利用して解くなど、なかなか想像しにくいかもしれませんが
ぜひチャレンジしてみてください。思わぬところでこれと同じような考え方が役に立つかもしれませんよ。
それでは、また。
お会いしましょう。