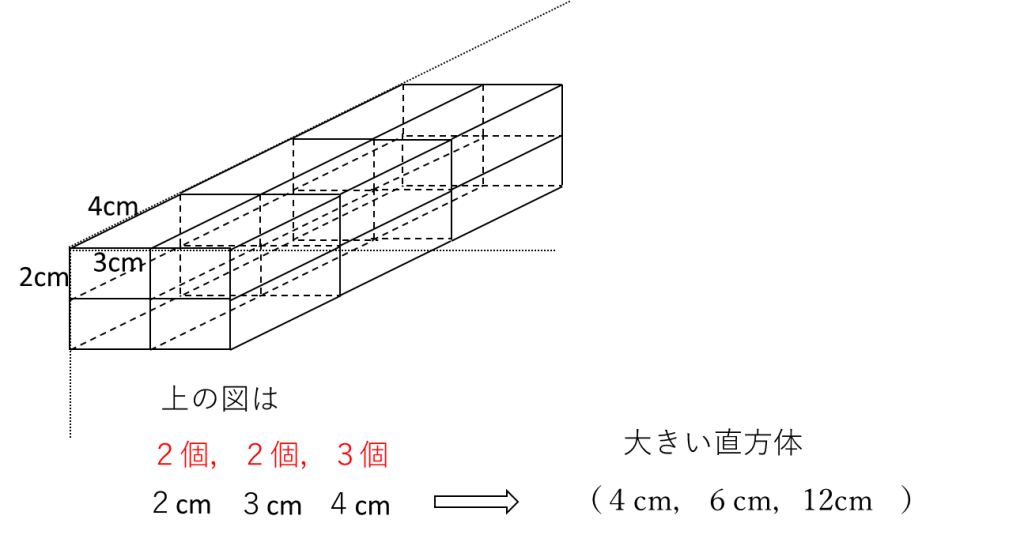みなさん、こんにちは。
受験Dr.の坂井です。
今回は書き出して調べてみる問題にチャレンジしてみましょう。
問題を解こうと思っていざ解き始めてみると、一見どこから手を付けて良いのかわからず困ってしまう人は多いのではないでしょうか。では、さっそく見てみましょう。
こんな問題。
【問題】
たて、よこ、高さがそれぞれ 2cm,3cm、4cmのレンガが12個あります。
これらをすべて同じ向きに積み上げて大きな直方体を作ります。
このとき、作ることができる大きな直方体の種類は何種類ありますか。
ポイントはどのように場合分けしていくかを考えることです。
レンガが12個あるということは、たて、よこ、高さに並ぶレンガの個数の積が12になればよいわけです。
まず、レンガの積み方を考えてみましょう。
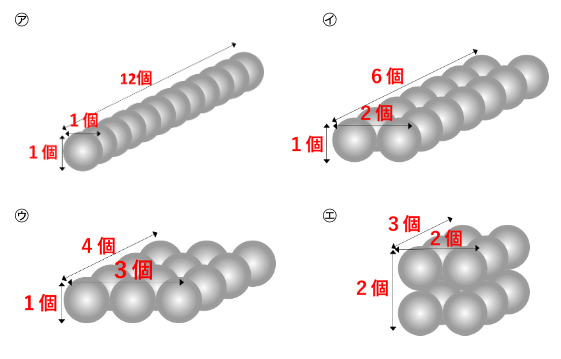
12 =1×1×12 ・・・・㋐
=1×2×6 ・・・・㋑
=1×3×4 ・・・・㋒
=2×2×3 ・・・・㋓
12を「たて×よこ×高さ」の形のかけ算で表すことができるのは
上の㋐~㋓の4種類です。それを図にしてみるの次のようになります。
次に㋐~㋓のそれぞれについて、重ねるレンガの向きを考えていきましょう。
≪㋐について≫
並べる向きをかえてレンガをつなげると次のような3種類の大きな直方体ができます。
(ⅰ)
2cm×3cmの長方形の面が手前にくるような向きでレンガを並べていくと
1辺が(2cm,3cm,48cm)という大きな直方体になります。
(ⅱ)
2cm×4cmの長方形の面が手前にくるような向きでレンガを並べていくと
1辺が(2cm,4cm,36cm)という大きな直方体になります。
(ⅲ)
3cm×4cmの長方形の面が手前にくるような向きでレンガを並べていくと
1辺が(3cm,4cm,24cm)という大きな直方体になります。
3種類は次のようになります。
1個 1個 12個 大きい直方体
2cm 3cm 4cm ⇨ (2cm,3㎝,48cm)
2cm 4cm 3cm ⇨ (2cm,4㎝,36cm)
3cm 4cm 2cm ⇨ (3cm,4㎝,24cm)
≪㋑について≫
並べる向きをかえてレンガをつなげると全部で6種類の大きな直方体ができます。
そのうち、1つの例を下図に示しました。
6種類は次のようになります。
1個 2個 6個 大きい直方体
2cm 3cm 4cm ⇨ (2cm,6㎝,24cm)
2cm 4cm 3cm ⇨ (2cm,8㎝,18cm)
3cm 2cm 4cm ⇨ (3cm,4㎝,24cm)
3cm 4cm 2cm ⇨ (3cm,8㎝,12cm)
4cm 2cm 3cm ⇨ (4cm,4㎝,18cm)
4cm 3cm 2cm ⇨ (4cm,6㎝,12cm)
≪㋒について≫
並べる向きをかえてレンガをつなげると全部で6種類の大きな直方体ができます。
そのうち、1つの例を下図に示しました。
6種類は次のようになります。
1個 3個 4個 大きい直方体
2cm 3cm 4cm ⇨ (2cm, 9㎝,16cm)
2cm 4cm 3cm ⇨ (2cm,12㎝,12cm)
3cm 2cm 4cm ⇨ (3cm, 6㎝,16cm)
3cm 4cm 2cm ⇨ (3cm,12㎝, 8cm)
4cm 2cm 3cm ⇨ (4cm, 6㎝,12cm)
4cm 3cm 2cm ⇨ (4cm, 9㎝, 8cm)
≪㋓について≫
並べる向きをかえてレンガをつなげると全部で3種類の大きな直方体ができます。
そのうち、1つの例を下図に示しました。
3種類は次のようになります。
2個 2個 3個 大きい直方体
2cm 3cm 4cm ⇨ (4cm,6㎝,12cm)
2cm 4cm 3cm ⇨ (4cm,8㎝, 9cm)
3cm 4cm 2cm ⇨ (6cm,8㎝, 6cm)
以上より、3+6+6+3=18種類あることがわかりました。
ここで、最後に注意しなければならないことが、同じ種類の大きな直方体がないかをチェックすることです。
18種類の中でダブってカウントしていないかを調べてみると…。ありましたね。
あらかじめ色を付けておいたのは、同じ種類の大きな直方体です。
これら4種類のダブりを取り除くことを忘れないでください。
18-4=14種類
それでは、また。
お会いしましょう。