こんにちは。
受験Dr.の小蔦です。
今回のお話はカタラン数。
カタラン数とは・・・。
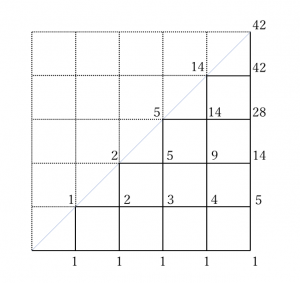
下の図でA地点からB地点まで最短距離でいくための道順は、14通りです。
そこに出てくる対角線上の数、1、2、5、14、42、(132)、(429)、・・・・と続く数が
カタラン数といわれる数です。
カタラン数にまつわるお話で有名なお話の1つに
こんな問題があります。
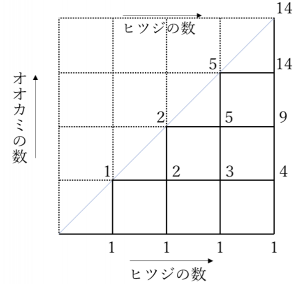
4匹のヒツジと4匹のオオカミがいます。
ヒツジたちとオオカミたちを檻にいれて運びたい。
でもヒツジとオオカミの檻に入れる順番を間違えると、ヒツジたちはオオカミたちに食べられてしまいます。
ヒツジたちがオオカミたちに食べられないようにするためには、
檻の中にいるヒツジの数よりオオカミの数が多くならないように入れていかなければなりません。
ヒツジの数とオオカミの数が同数の場合は、何とか食べられずにすみます。
では、ヒツジたちがオオカミたちに食べられないように檻の中に入れる方法は何通りあるでしょうか、という問題です。
これは、最短距離で進む方法を求める道順の図を用いて説明ができます。
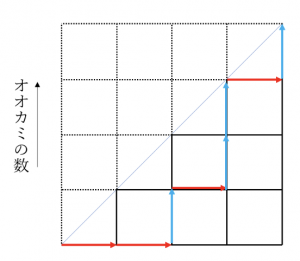
対角線上より下側は檻の中に入っているヒツジの数がオオカミの数より多い領域となります。
ですから対角線上も含む、対角線上より下側の領域を通って点Aから点Bまで進む最短距離の進み方がヒツジたち、オオカミたちをヒツジがオオカミに食べられることなく檻の中に入れていくことが可能な入れ方になっています。
右の図は、①ヒツジ②ヒツジ③オオカミ④ヒツジ⑤オオカミ⑥オオカミ⑦ヒツジ⑧オオカミの順に入れた様子を表しています。
すべての可能な入れ方を考えると下の図のようになります。
よって檻の中への入れ方は14通りであるとわかります。
次の問題も同じように考えることができます。
ぜひチャレンジしてみてください。
【問題】
あるラーメン屋では毎週水曜日にすべてのメニュー500円セールを実施しています。
ある水曜日、開店前に8人の客が待っていました。8人の客のうち4人は500円玉だけ、
他の4人は1000円札だけを持っていました、このラーメン屋ではおつりに使う硬貨が1
枚もなかったので、おつりが不足しないように500円玉と1000円札を1人ずつもらう順
番を工夫して販売しました。このとき、500玉と1000円札をもらう順番は全部で何通り
ありますか。ただし、8人の客はそれぞれ1品しか注文していません。
14 渋谷幕張中改題
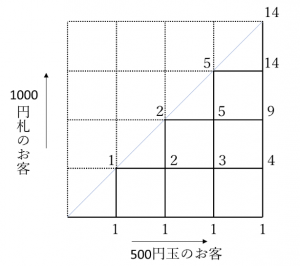
おつりが払えるような順番を考えます。例えば、最初に500円玉を持っているお客が来れば
つぎに1000円札を持っているお客が来てもおつりを渡すことができます。
1人目500円玉、2人目500円玉、3人目1000円札というようにお客が来てもおつりを払うことができるので大丈夫です。
しかし、1人目500円玉、2人目1000円札とお客が来た場合、次の3人目で1000円札を持ったお客が来ても渡すおつりがないのでこの順番ではだめです。
つまり、来たお客の数が、500円玉をもったお客より1000円札のお客の数が多くならないようにすればいつもおつりが渡せる状態になるのです。
これはヒツジとオオカミを檻の中に入れる順番を考える方法と同じ考え方で解決できます。
ということで14通りであることがわかります。
カタラン数に関する問題は、中学入試で1990年代から多く出題されはじめ、今もなお多くの学校で出題されている題材です。
ぜひ興味を持って取り組んでみてください。
それでは、またお会いしましょう。