皆さん、こんにちは。
受験Dr. の坂井です。
今回は、どうやって「計算ミス」をなくすのかをお伝えしていきます。
「計算ミスしない!」「慎重に解きなさい!」
私も受験生時代、散々言われた言葉です。
受験生はそれに対して「わかったよ」としか返答のしようがないのです。そして、この会話のやり取りは、時間の浪費を生むばかりで計算力が上がることは決してないわけです。
「しっかり」計算する。
「ミスしないように」計算する。
そんなことは受験生自身が十二分にわかっていることです。
テスト中は全力でそうしたいと思って取り組んでいることでしょう。
でも、また同じことを繰り返す・・・・
「計算ミスが多くって・・・」と相談を受けたとき、よく問題用紙を見せていただくことにしています。
余白部分の計算過程を見るためです。
すると一生懸命お子さんたちが戦った計算過程が書きこんであるのですが、
実は本当の「計算ミス」ではないことが多いです。
これは、あくまでも持論ですが、
計算ミスとは
①繰り下がりのミス
②解答用紙に答えを転記するときの書き間違え
受験生自身の自覚で直せる
③汚い数字による見間違え
そして上級者でも起こりうる
④「うっかり」
くらいなのではないかと私は思っています。
それら以外の「ミス」と評価されているうちの多くの原因は、
知識不足によるものであり、本当の「ミス」ではありません。
見せていただく問題用紙に書き込んである計算過程を見ると、知っていれば一瞬で処理できるものを「知らない」ことが原因で多くの手順を踏んでいるものが非常に多くみられます。
余計な手順を踏むことは、より計算が複雑になったり、時間を必要以上に使うことになったりするのです。
そうしているうちに「計算間違い」が起こります。
必要以上に時間がかかってしまうことは、知らず知らずのうちに受験生の「焦り」を生みます。
軽いパニックです。
そしてどの受験生も計算問題(大問1)が終わった時点で必ず残り時間を確認します。
「あ~ こんなに時間を使ってしまった・・・。」
これがさらに大問2以降への焦りの「スイッチ」になるのです。
大問2以降の問題で、『テストでは解けなかったけど家で解き直したらすぐ解けた』なんてことをよく耳にします。
もしかすると「スイッチ」がオンになってしまったことが原因かもしれません。
「しっかり計算しなさい。」っていつも言ってるんですけど・・・・。
保護者からよく聞く言葉です。
これ、言ったことない保護者っているんでしょうか。
言っちゃいますよね。
その会話をきっかけにバトル勃発という流れも多いのでは・・・。
計算ミス(本当のミスではない、計算間違いのこと)を減らすには知識が必要です。
知識が十分にない状態でいくら気を付けて計算を行っても、どうしても手順が多くなり
間違いの発生する可能性が高くなります。
そして時間を多く使ってしまうことにより 「焦り」 を生みます。
テストが始まる ⇒ 計算問題に取り掛かる。
⇒ 手が止まるかまたは計算過程が多くなる ⇒ 想像以上に時間がかかる
⇒ やっと計算が終わり時計をみたら、もうこんなに時間がたっていた ⇒ 焦る
この時点で、平静な状況ではなくなっています。
冒頭で述べた
①繰り下がりのミス
②解答用紙に答えを転記するときの書き間違え
これらのミスは、慌てず焦らず取り組むことができれば減らせることができます。
「しっかり」「気を付けて」で直せるものではないのです。
そのためには、計算をスピディーかつ正確に解けるようになることが必要なのです。
ひたすら計算練習をすることも重要ですが、それに加え必要な知識を十分に活用した練習が安定した計算力を育てます。
では、必要な知識とは何か。
①小数・分数の換算
③3.14の計算の答えの暗記
③繰り下がりのある分数の引き算
⇒ 仮分数に直さないで計算(仮分数に直すとかなり時間がかかる)
④帯分数×整数の計算
⇒ 仮分数に直さないで計算(仮分数に直すとかなり時間がかかる)
⑤平方数の暗記
⑥三角数の暗記
⑦速さの換算方法
などなど・・・たくさんあります。
今回はこの中で、計算問題を解くうえで使用頻度の高い
①小数・分数の換算 をお伝えします。
計算過程で小数を分数に一瞬で換算できれば、間違えることなく時間をかけずに計算できるので、その分心にゆとりも持てます。
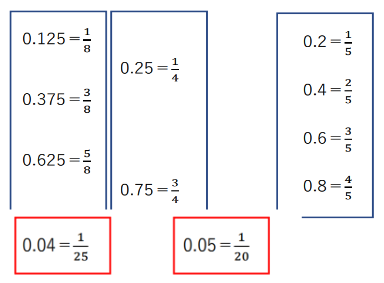
小数⇔分数の換算
下の青い枠で囲まれた小数⇔分数は、覚えている人も多いのではないでしょうか。
それに加えてもう1つ赤い枠で囲んだ小数⇔分数も換算方法を覚えたほうが良いでしょう。
赤い枠で囲まれた分数は、小数第1位,第2位の小数点以下の数が4の倍数のものと5の倍数のものです。例えば、0.24と0.85を分数に直してみましょう。0.24の小数点以下の数「24」は「04」の6倍なので
![]() の6倍の
の6倍の ![]() となります。そして0.85の小数点以下の数「85」は「05」の17倍なので
となります。そして0.85の小数点以下の数「85」は「05」の17倍なので ![]() の17倍の
の17倍の ![]() となります。
となります。
これらを普段の計算練習の際、積極的に活用してください。
「時間をかければ答えが出るから大丈夫・・・」では、テストで計算を解いているときに
余計に時間をかけることになってしまいます。
次の問題が1分くらいでできるようになることが目標です。
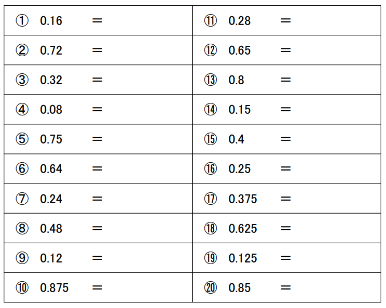
【問題】
次の①~⑳の小数を分数に直しなさい。
どうですか。慣れるまでは時間がかかりますが、積極的に活用を意識しながら普段の計算練習に取り組んでいけたら、1分くらいでできるようになります。
ぜひチャレンジして習得してください。
それでは、またお会いしましょう。