皆さん、こんにちは。
受験Dr. の坂井です。

計算ミスをなくす・・・・。
これはどの受験生も抱えたことがある悩みの１つではないでしょうか。

「しっかり」計算する。
「ミスしないように」計算する。

そんなことはどの受験生も思っていることだし、ましてやわざとミスをする人もいないわけです。
それでも、多くの受験生の悩みにタネとして登場してくるのが

「計算ミス」をどうやって減らしていけばよいのか・・・・・　です。

前回のブログでは、「計算ミス」をなくすための「知識を活用」することによる技術面をブラッシュアップさせることで計算ミスをなくしていくという手段をお話しました。
計算過程のなかで頻出する「分数 ⇔　小数」の換算方法をブラッシュアップさせることにより、時間をかけることなく一瞬で処理し、かつ正確な答えを出すといったものでした。

今回は、「繰り下がりのある分数の引き算」　と　「帯分数×整数」　　の計算方法をお伝えしていきます。

ひたすら計算練習をすることも重要ですが、それに加え必要な知識を十分に活用した練習が安定した計算力を育てます。

たかが分数の引き算とかけ算ではないか・・・・。　と思うのですが、
この計算、　「計算ミスが多い」と悩んでいる受験生の多くが遠回りしてかなり時間がかかる方法で計算しているのが現状です。　4年生、5年生はいまのうちに計算方法を習得しておきましょう。

 

繰り下がりのある分数の引き算　（帯分数を仮分数に直さない）

分数の引き算の際に、なんでもかんでも帯分数を仮分数に直してから計算する受験生が多くいます。

例えばこんな計算です。

 

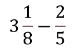
まず　　を仮分数に直してから通分して計算します。

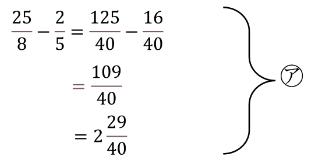
こんな感じで計算が進んでいるはずです。

これを仮分数に直さない計算方法だと次のような計算手順になります。

この時点で、　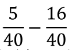　の分子の「５から１６が引けない」のを嫌って、㋐のように仮分数に直してから計算したくなってしまうのでしょう。

しかし、ここで仮分数に直さず、「繰り下がり」の考え方を利用してみると

と変換することができます。

すると、次のようになります。

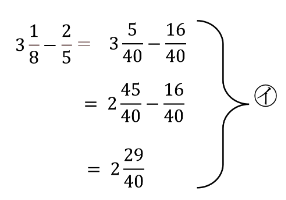
㋐と㋑を比べると、これだけの計算過程で㋐より㋑の方が２手分、計算手順が少ないことがわかります。
①仮分数に直す　②引き算した後の仮分数を帯分数に直す　　という2手です。
比較的簡単な分数の引き算を例にしましたが、6年生の夏以降にもなると、数がもっと大きくなったり、計算しづらい数値が出てくるわけですから、なおさら手順は少ない方がミスする場面が減るわけです。

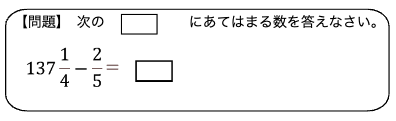
次の計算を㋐㋑の両方の計算方法で解いてみてください。
計算にかかる負荷が異なることがより一層はっきりすることでしょう。

 

 

【帯分数 × 整数　　（仮分数に直さない）　】

帯分数　×　整数の計算も帯分数を仮分数に直して計算する場合と、仮分数に直さずに計算する場合では、計算にかかる負荷にだいぶ差があります。

例えばこんな計算です。

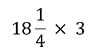
を仮分数に直してから計算すると、次のような手順になります。]

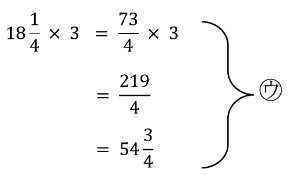
このような計算手順でテストの余白に計算過程が書かれている受験生は多いのではないでしょうか。

これを仮分数に直さないで計算するとこうなります。

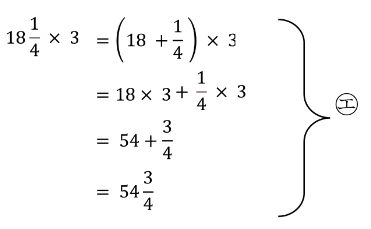
説明のために㋓も４行の計算過程を記しましたが、仮分数に直さないで計算すれば暗算で計算できてしまう受験生も多いのではないでしょうか。

では、次の計算も㋒㋓の両方の計算方法で解いてみてください。
これも計算にかかる負荷が異なることがより一層はっきりすることでしょう。

 

 

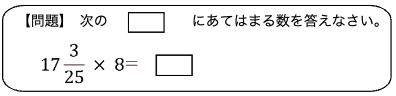
どうですか。計算にかかる時間、計算のしやすさ、計算の正確性のいずれも仮分数に直さないほうが圧倒的有利に計算できるといえるでしょう。

今回は、「繰り下がりのある分数の引き算」　と　「帯分数×整数」　において仮分数に直さないで計算するという計算技術についてお伝えしました。
「計算」の技術面をブラッシュアップさせることで計算ミスを減少させ、また、時間をかけずに計算できることで心にゆとりをもたせることができ、テスト中の「焦り」の発生を防ぐことにもつながってきます。
是非、普段の計算練習の際に積極的に取り入れて習得してください。

それでは、またお会いしましょう。