皆さん、こんにちは。

受験Dr. の坂井です。

 

前回、前々回に続いて、　「計算ミスをなくす・・・」ためのお話の第3弾です。

 

「気をつけて」計算すれば・・・、

「一所懸命」計算すれば・・・　　果たして計算ミスは減らせるのかといったお話です。

 

「気をつけて」とか「一所懸命」で計算ミスが減らせないのが現状です。

だってどの受験生も、気をつけてかつ一所懸命にテストに臨んでいるのですから・・・・。

ましてやわざと計算ミスをする受験生なんて皆無なわけです。

 

「気をつけて」や「一所懸命」などの気合みたいなもので本当に計算ミスがなくなるのであれば、

どうぞお子さんたちを目いっぱい叱ってあげてください。

でもそんなお声がけは不毛なバトルの引き金になるだけで、何の解決にも至らないことは明白ですね。

 

計算ミスをなくすためには、技術面（知識）をブラッシュアップさせることが必要です。

ミスを防ぐための強化するべき技術のうち、今回は3.14に係るお話をします。

 

3.14の計算は絶え間なく受験生の目の前に現れます。

３．１４に係る計算でミスをなくすためには、計算にかかる負荷を減らすことが必要です。

それでは負荷を減らすために必要な技術（知識）とはどんなものなのかを見ていきましょう。

 

計算結果を覚える

3.14の計算は計算結果を覚えておくことが必要不可欠です。

ひっ算をすれば答えは出せますが、それにかかる時間と正確性を考えると計算結果を覚えておくことが断然有利です。さらに多くの受験生が計算結果を覚えている以上、その都度ひっ算をして戦う方法は明らかに不利であるといえるでしょう。

2×3.14＝6.28

3×3.14＝9.42

4×3.14＝12.56

5×3.14＝15.7

6×3.14＝18.84

7×3.14＝21.98

8×3.14＝25.12

9×3.14＝28.26

12×3.14＝37.68

15×3.14＝47.1

これらの計算結果をまず覚えてください。

そして、面積で頻出する以下の計算もあわせて覚えておくと良いでしょう。

2×2×3.14＝12.56

3×3×3.14＝28.26

4×４×3.14＝50.24

5×5×3.14＝78.5

6×6×3.14＝113.04

8×8×3.14＝200.96

 

そして、計算結果を覚えた状態で問題を多く解いてください。

 

まとめて計算

求積問題での3.14の計算は、その都度計算結果を算出するのではなく、

いかにまとめて3.14の計算を行うかがポイントです。

 

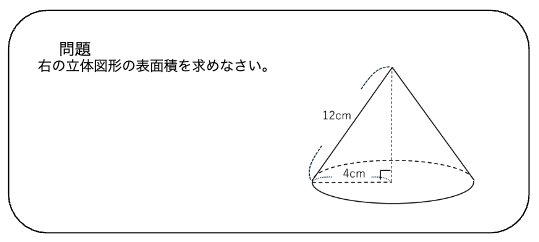
側面積と底面積に分けて計算します。

 

＜側面積＞　母線　×　半径　×　3.14

　１２　×　４　×3.14　＝　１５０．７２（ひっ算）

＜底面積＞

　４ × ４ × 3.14 = 50.24（ひっ算）

よって表面積は、　１５０．７２　＋　５０．２４　＝　２００．９６（㎠）　　となります。

 

これは間違った方法ではありませんが、３．１４の計算をその都度算出しています。

このくらいの計算量でしたら、ミスはしないかもしれませんが、計算過程がより多くなるにつれて計算手順が増え、それらを集計するための時間がかかり、それに伴いミスが発生する可能性が増えていきます。

実際、３．１４の計算をその都度算出している受験生は、例外なく計算ミスが多く、また必要以上に計算時間がかかりすぎているようです。

その都度算出するのではなく、まとめて計算すると次のようになります。

 

＜側面積＞　母線　×　半径　×　3.14

　１２　×　４　×3.14　＝　４８ × 3.14

＜底面積＞

　４ × ４ × 3.14 = 16 ×　３．１４

よって表面積は、　（４８　＋　１６）　×　３．１４　＝　６４　×３．１４

＝　200.96(㎠)　←もちろん計算の答えは知っているので計算は

行いません。暗算です。

 

計算問題

逆算・工夫が必要な計算問題では、3.14の計算結果をまともに計算してしまうと

計算量が膨れ上がり、時間もかかってしまうことが多いです。

 

□＝①　と置いてみます。

　　すると　　①×3.14　＋　②×3.14　－　3×3.14　＝　37.68　　　となります。

まともに計算すると、　③×3.14　＝　９．４２　＋３７．６８

　　　　　　　　　　　　　　　　　　　　　　　　　　 ＝ 47.1

このあと①の値をもとめるために

４７．１　÷　３.１４ ÷ 3　の計算を行うことになります。

 

では、計算結果を知っている受験生の計算過程はどうなるでしょう。

次のようになります。

37.68が　12×3.14　であることを知っているので、

③×3.14　＝　３×3.14　＋　１２×３．１４

　　　　　　　　　＝　１５×３．１４

まで、容易にたどり着けます。

あとは　③＝15　だから　①＝５　つまり、　□＝５　と正確に短時間で算出できます。

この両者を比べるだけでも、計算手順、正確性、計算にかかる時間がだいぶ異なります。

後者の方は、受験生自身も解いた答えが多分正解であろうと思いながら次の問題に取り掛かれます。

時間も短時間で解けているので平常心を保ちながらそれ以降の問題に取り組めることでしょう。

 

もし、この計算問題1問で時間をかけてしまったら、「焦り」のスイッチが無意識に入ってしまい、この後の問題を平常心で取り組めなくなるといったことも起こりうるかもしれません。

今回は3.14に係る計算のミスを減らすための

①　３．１４の計算結果を覚える

② ３．１４の計算はまとめて集計する

といった技術面（知識）についてのお話でした。

 

ぜひ学習に取り入れていただき、自信をもって計算・集計ができるようになっていただければ幸いです。

５年生は夏期講習前までには３.１４の計算結果を言えるようにしておきましょう。

 

それではみなさん、

またお会いしましょう。