皆さん、こんにちは。
受験Dr.の坂井です。

5年生は9月以降、比についての本格的な学習が始まりました。
5年生の前期までに学習した内容について比を利用して解いていくことになります。
今回は、自由自在に“比の利用”を活用できるようになるための、根本原理をお伝えします。
算数で登場してくる数量関係の多くは、以下に示す3量の関係で構成されています。

1． たて×よこ＝面積
2．　底辺×高さ(×1/2)＝面積
3．　(上底+下底)×高さ(×1/2)＝面積
4．　対角線×対角線(×1/2)＝面積
5．　底辺×高さ＝面積
6．　底面積×高さ＝体積
7．　底面積×高さ(×1/3)＝体積
8．　底面積×平均の高さ=体積
9．　1枚あたりの金額×枚数=金額合計
10．　1個あたりの代金×個数＝代金合計
11． 間隔×間の数＝きょり
12． 濃さ×食塩水＝食塩
13． 1時間あたりの仕事量×時間＝仕事量
14． 歯数×回転数=通過する歯数
15． 速さ×時間＝きょり
16． 歩幅×定時間内の歩数＝きょり(速さ)
17． 平均点×人数(個数)＝合計点数

これらの中から、いくつか例にとって、どのように比を利用していくのかを見ていきます。

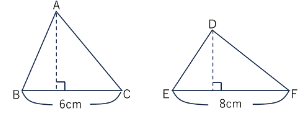
三角形ABCと三角形DEFの高さを実際に求めてから比を求めてみます。
三角形ABCの高さは、　30×2÷6＝10（ｃｍ），　　三角形DEFの高さは、16×2÷8＝4（cm）
よって　10：4＝5：２　と求めることができました。

今度は、実際の面積、辺の長さを用いずに比を利用して2つの三角形の高さの比を求めてみましょう。

まず。三角形の面積で登場する3量の関係は、

底辺×高さ× =　面積　　　です。

2つの三角形の底辺の比は　3：4，　　面積の比は15：8です。
高さの比は、　15÷3＝5，　　8÷4＝2　となります。
よって、上の表のように2つの三角形の比は　5：2　となります。（上の表を参照）

この問題に登場してくる3量の関係は、

間隔×間の数＝きょり　　です。

木と木の間の間隔　×　間の数　＝　池のまわりの長さ　になります。
このとき、木の本数と間の数は等しいことに注意しましょう。

5ｍおきに木を植えるときも3ｍおきに木を植えるときも同じ池の周りに植えるわけですから
池の周りの長さは等しくなります。
よって木の本数の比は間隔の比の逆比である3：５となります。（下の表を参照）

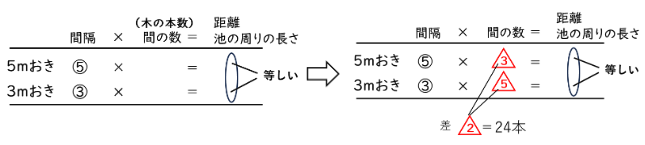
さらに本数の差が24本だから，5ｍおきの場合は36本（間の数は36か所），　3ｍおきの場合は60本（間の数は60か所）であることがわかります。（下の表を参照）

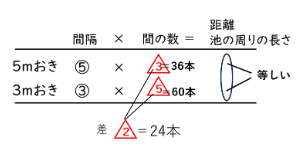
よって池の周りの長さは，　5ｍ　×　36か所　＝180ｍ　または　　3ｍ　×60か所＝180ｍ　となります。

登場する3量の関係は、
1枚あたりの金額×枚数=金額合計　　となります。

50円玉と100円玉の硬貨1枚あたりの金額の比は1：2です。
3量の関係を表にして表すと次のようになります。

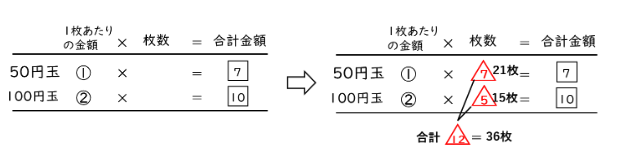
7÷1＝7,　　10÷2＝5　だから，
50円玉と100円玉の枚数の比は，　7：5　となります。
枚数の合計が36枚だから、50円玉と100円玉の枚数は，　21枚と15枚です。
よって，　50円玉の合計は　50円×21枚＝1050円，　　100円×15枚＝1500円
貯金箱の中にある金額の合計は，　1050＋1500＝2550円となります。

比の利用について3つの例をあげましたが、学習する際のコツは、
その問題に登場する3量の関係を把握することです。

やみくもに問題練習するだけではなく、早く自由自在に比の利用を活用できるようになるには、
冒頭であげた17種類の3量の関係が頭の中にすぐに出てくることが必要です。

5年生のみなさん、6年生になる前にぜひ「比の利用」が得意になれるように頑張ってください。
応援しています。

それではみなさん、またお会いしましょう。