みなさん、こんにちは。
受験Dr.の坂井です。
受験算数において、図形分野の学習は入試問題で頻出単元であることもあり、受験生にとっては避けて通ることができない重要な単元です。学習する中で求積問題に関連する内容で初めに学習するものは長方形、正方形の面積ですが、続いて三角形の面積について学習することになります。
三角形の面積が単元学習として登場してくるのが4年生です。「うちの子は図形分野が苦手で・・・」というお悩みを聞くことが多くありますが、受験生が図形分野に苦手意識を感じるのはこの段階からである可能性があります。
三角形の面積を求めること自体は難しくありません。なぜなら、三角形の面積を求めるための公式を学習する際に暗記するからです。公式に当てはめて答えを出すことで学習を開始した当面は答えを出すことに苦労はしません。しかし、学習が進んでいくと模擬試験で出題される問題のレベルは、公式に当てはめて答えを出せていたはずの三角形の面積を求める問題から、やがて本質まで理解していないと解答することができないレベルまですぐに難易度が上がってしまうのです。公式に当てはめるだけの学習をしている4年生はそのあと学習する「等積変形」という概念の本質的理解も応用することが難しくなり、やみくもに問題演習だけを増やすという応用力が養成できない学習手段に陥る可能性が生じてきます。練習のときは解けていたがテストになるとできないといった現象が起きるのも、こういったことが原因になっていることが多いのです。
三角形の面積を学習する際に、面積を求めるための公式を覚えることはもちろん重要ですが、そこに本質的理解が備わっているかどうかが重要です。
三角形の面積=底辺×高さ÷2
というのが三角形の面積を求める公式ですが、公式の暗記だけに頼らない本質的な理解とはいったい何なのか、学習する際におさえなければならないポイントをお伝えします。
【学習する際におさえるべきポイント】
1 底辺と高さは垂直な位置関係にあること
2 2種類の三角形の高さがどこにあたるのかを理解すること
以上の2点です。
2種類の三角形とは次の図1,図2のように分類されます。
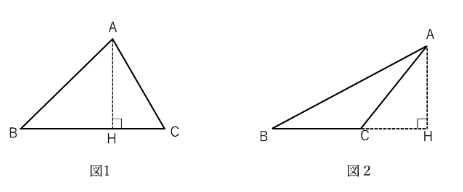
図1は頂点Aから下した垂線の足である点Hが底辺BC上にあるもの
図2は頂点Aから下した垂線の足である点Hが底辺BC上にないもの
図1の場合は、どれが底辺でどれが高さであるのかを間違える受験生はほとんどいません。面積の計算で間違えるとしても、うっかり底辺×高さを計算したあと、2で割るのを忘れてしまったといったところでしょう。
ところが、図2のような三角形になったとたん、様子が変わることがしばしば見受けられます。どれが高さになるのかが見えなくなるのです。
どれが高さになると思うかと生徒に聞くと、下図の赤線が高さにみえてしまう受験生たちがいます。
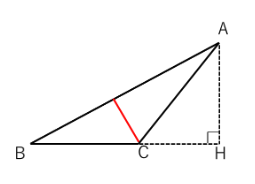
そして、赤線の長さがわかっていないから面積が計算できないといって困ってしまうのです。
【指導する際の注意点】
受験生がそのような状況になったら、辺BCが底辺で、それと垂直になっているのがAHだからAHが高さになるという指導は避けたほうがよいでしょう。
言われたその場では、AHを高さにして計算することはしてくれますが、受験生の感覚では赤線が高さに見えているのです。時間がたつとまた同じような間違えを繰り返す可能性があるでしょう。再度間違えることにより、AHがBCに垂直だから高さになるという指導をまた受けることになります。要は、あまり納得がいっていないことを繰り返し指導され、理解に到達することが難しくなっていきます。そして苦手意識が芽生えてくるのです。
三角形の底辺と高さは垂直になっていなければなりませんが、垂直になっているからこの部分が高さになるといった指導では腑に落ちない4年生が多くいるのも事実です。
三角形を方眼紙に作図し、それを受切り取って実際の面積と一致することを受験生と一緒に確認するといった方法でもよいでしょう。
または、三角形ABHの面積から三角形ACHの面積をひいて実際の面積と等しくなることを受験生と一緒に確認するといった指導も効果的です。
また、平行四辺形の面積の求め方を学習した後に、以下の①②を利用して再度理解の確認をしてみるのもよいでしょう。
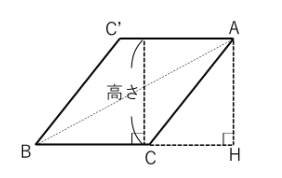
1 三角形ABCの面積は平行四辺形AC‘BCの面積の半分
2 平行四辺形の高さであるCC’はAHと同じ長さであること
自分の感覚と本質的理解が一致するといった状態で正解まで到達できることは受験生たちにとって小さな成功体験ともいえるでしょう。この小さな成功体験を積むことは非常に重要なことです。自己肯定感が高まり、より難しい問題に挑戦したいという意欲が湧いてきます。達成感を味わうことで、自信がつき、学習意欲が高まります。小さな成功体験を積み上げることが、最終的には大きな成功へとつながっていくのです。
2月より始まった新学年の学習で、みなさんの小さな成功体験が積み重ねていけるよう応援しています。
それでは、またお会いしましょう。




