こんにちは。
受験Dr.の坂井です。
2月入試まで70日を切りました。
受験生のみなさん、風邪などひかぬようにしてお過ごしください。
今回は、入試でもおなじみの「円すい台の表面積」について確認していきます。簡便法を利用した方法もあわせてみていきます。
早速ですが、こんな問題。
下の図のような円すいを下から
の高さで底面に平行な面で２つの立体を切り分けました。このとき切り口の下側にできる立体の表面積を求めなさい。
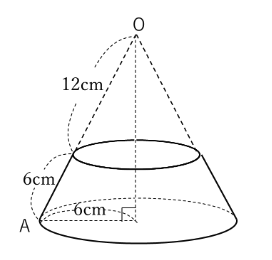
簡便法とは、求める表面積のうち、側面積の部分を簡便的に求める方法です。
まずは、簡便法を利用しない解き方、一般的な解き方を見ていきましょう。
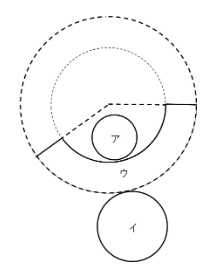
ア：切断の切り口の部分になります。
相似比を利用して、半径は４㎝とわかります。
4×4×3.14＝16×3.14（㎠） ☜ 計算結果は出さずにこのままにしておきます。
イ：底面になります。半径は6cmですので
6×6×3.14＝36×3.14（㎠） ☜ 計算結果は出さずにこのままにしておきます。
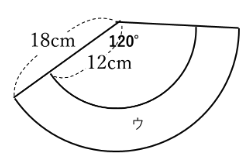
切断する前の円すいを展開図にしたときの側面の中心の角度は120°になります。
ウの部分の面積は、半径18cm、中心の角度が120°のおうぎ形から半径12㎝、中心の角度が120°のおうぎ形をひいたものになります。（右図(下図)）
☜ 計算結果は出さずにこのままにしておきます。
よって、
ア＋イ＋ウ ＝（16＋36＋60）×3.14
. ＝ 112×3.14
. ＝ 351.68（㎠） となります。
☜ まとめて計算一気に計算しましょう
この計算方法でも丁寧に計算していけば、特別時間がかかるわけでも、計算過程が多くなるといったことにはならないでしょう。ですから、入試直前期を迎える6年生は、しっかりこの計算方法をマスターしてください。簡便法は別解程度に考えてください。
これから学習する5年生はぜひ簡便法も参考にしてほしい方法です。
簡便法（別解）
側面の面積（ウの部分）を求めるときに簡便法を利用していきます。
側面の部分を台形とみなして、台形の面積を求めに行くつもりで計算する方法です。
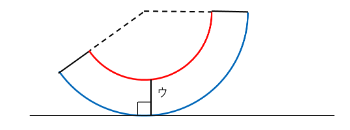
上の図の赤い線を台形の上底、青い線を台形の下底と考えます。
そして赤い線と青い線との距離を台形の高さとみなします。
赤い線の長さ：12×2×3.14×
＝8×3.14（cm）・・・・・・台形の上底
☜ 計算結果は出さずにこのままにしておきます
青い線の長さ：18×2×3.14×＝12×3.14（cm）・・・・・台形の下底
☜ 計算結果は出さずにこのままにしておきます
高さ ：18-12＝6（cm）
では、台形の面積を計算してみましょう。
（8+12）×3.14×6×
＝60×3.14 ・・・・ウの部分
☜ 計算結果は出さずにこのままにしておきます
これに、ア，イの面積を合計すると
ア＋イ＋ウ ＝（16＋36＋60）×3.14
. ＝ 112×3.14
. ＝ 351.68（㎠） となります。
☜ まとめて計算一気に計算しましょう
入試で、立体図形や平面図形で計算ミスに気をつけなければいけない代表例が、この円周率に関連する計算です。
1ケタ×3.14の計算結果は暗記しておく方が圧倒的に有利です。答えを正確に覚えていれば試験中に行う計算回数が減るばかりではなく、正確な計算結果を得られるからです。
できれば、半径×半径×3.14の計算結果も半径が２～９cmのものについては覚えた方がよいです。
どうしても覚えることが難しいという受験生は、1ケタ×3.14の計算結果は確実に覚えるようにしましょう。
3.14が関連する計算の心得
①1ケタ×3.14の計算結果を正確に覚えましょう。
②3.14の計算は、計算結果をその都度計算して出すのではなく、できるだけまとめて計算するようにしましょう。
心得としてはこの２点に尽きると思います。入試本番はおそらく通常以上に緊張した状態で問題を解くことになるでしょう。その緊張した状態でも確実に正解を出すために6年生は入試までの残りの時間で3.14に関連する計算に自信がもてるよう準備していきましょう。
それでは、またお会いしましょう。
