こんにちは。
受験Dr. の坂井です。
前回のV形の並べ方に引き続き、今回はW形の並べ方について考えていきましょう。
W形に並べるとはどんな並べ方なのか。
前回のV形と同様に、数の大きさが大きいほど下に位置し、上に行くほど小さくなるような並べ方です。
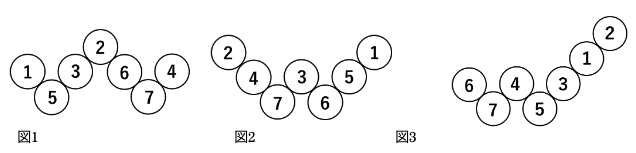
例えば、1~7の数でW形に並べると図1や図2に示すような並び方になります。
1から7までの数の中で最も大きい数が7ですから、7がW形の最も下に位置することになります。
図1ではW形の一番左は1ですが、これは1<5だから1は5より小さい数なので5より上側に並べることができます。一番右の4も4<7だから4は7より小さいので7より上側に並べることができます。
2と3については、5>3>2と上に位置するほど数の大きさが小さくなっていきます。
2と6についても、7>6>2と上に位置するほど数が小さくなっていきます。
一方、図3を見るとW形の右側が5<3<1までは上に位置するほど数が小さくなっていきますが、1より大きい2が1より上に並んでいるので、このように並べることはできません。
W形の並べ方のルールがわかったところで、いよいよこのようなW形の並べ方が何通りできるのかを考えていきましょう。
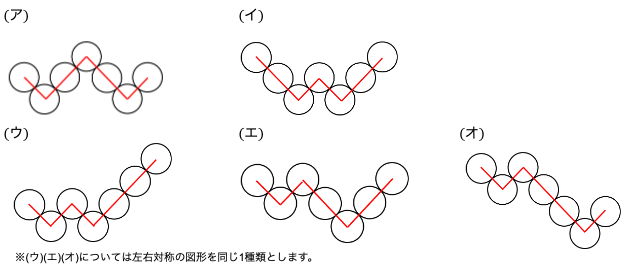
1から7までの数で並べる場合、W形の並べ方は下図の(ア)~(オ)のような5種類の形があります。
場合分けをしながら丁寧に集計していく必要があるため、やや難しいと思われますが
とても良い練習になります。じっくり取り組んでみてください。
今回は、これらのうち(ア)の形の並べ方について考えていきましょう。
(ア)について
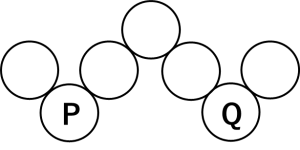
1~7の中で7は最大の数だから、7の位置は
右の図1のPまたはQとなります。
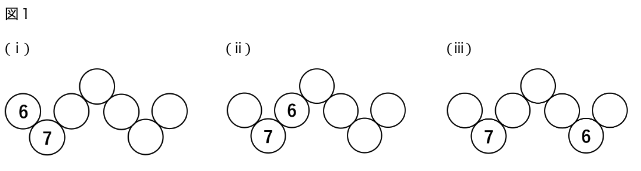
7がPの位置にあるとき、6の位置は次の3通りです。
(ⅰ)~(ⅲ)のそれぞれについて、場合分けをしながら並べ方が何通りあるかを考えていきましょう。
(ⅰ)の場合
1を並べることができる場所で場合分けして考えます。
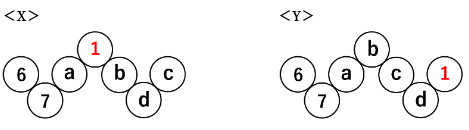
1を並べることができる場所は次に示す<X><Y>の2通りです。
<X>と<Y>の場合について、aの位置に並べる数によりそれぞれ何通りあるかを考えていきます。
<X>について
a=2のとき、(b,c,d)=(3,4,5)または(4,3,5)の2通り
a=3のとき、(b,c,d)=(2,4,5)または(4,2,5)の2通り
a=4のとき、(b,c,d)=(2,3,5)または(3,2,5)の2通り
a=5のとき、(b,c,d)=(2,3,4)または(3,2,4)の2通り よって 2×4=8通り になります。
<Y>について
aの位置に2を並べることができない(2より小さい1をbの位置に並べることができないから)ことに注意して、
a=3のとき、(b,c,d)=(2,4,5)の1通り
a=4のとき、(b,c,d)=(2,3,5)の1通り
a=5のとき、(b,c,d)=(2,3,4)の1通り よって 3通り になります。
したがって、(ⅰ)の場合は、 8+3=11通り になります。
(ⅱ)の場合
(ⅰ)と同様に、1を並べることができる場所で場合分けして考えます。
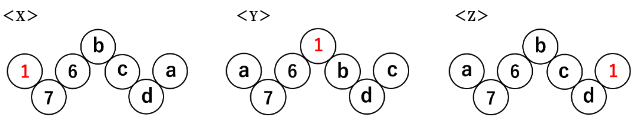
1を並べることができる場所は次に示す<X><Y><Z>の3通りです。
(ⅰ)と同様に、<X><Y><Z>の場合について、aの位置に並べる数によりそれぞれ何通りあるかを考えていきます。
<X>について
aの位置に5を並べることができない (5より大きい6または7をdの位置に並べることができないから)ことに注意して、
a=2のとき、(b,c,d)=(3,4,5)の1通り
a=3のとき、(b,c,d)=(2,4,5)の1通り
a=4のとき、(b,c,d)=(2,3,5)の1通り よって 3通り になります。
<Y>について
a=2のとき、(b,c,d)=(3,4,5)または(4,3,5)の2通り
a=3のとき、(b,c,d)=(2,4,5)または(4,2,5)の2通り
a=4のとき、(b,c,d)=(2,3,5)または(3,2,5)の2通り
a=5のとき、(b,c,d)=(2,3,4)または(3,2,4)の2通り よって 2×4=8通り になります。
<Z>について
a=2のとき、(b,c,d)=(3,4,5)の1通り
a=3のとき、(b,c,d)=(2,4,5)の1通り
a=4のとき、(b,c,d)=(2,3,5)の1通り
a=5のとき、(b,c,d)=(2,3,4)の1通り よって 4通り になります。
したがって、(ⅱ)の場合は、 3+8+4=15通り になります。
(ⅲ)の場合
(ⅰ)(ⅱ)と同様に、1を並べることができる場所で場合分けして考えます。
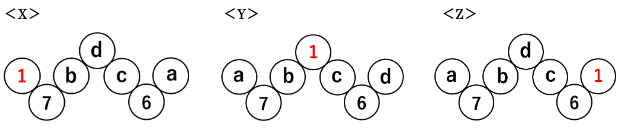
1を並べることができる場所は次に示す<X><Y><Z>の3通りです。
(ⅲ)も(ⅰ)(ⅱ)と同様に、<X><Y><Z>の場合について、aの位置に並べる数によりそれぞれ何通りあるかを考えていきます。
<X>について
a=2のとき、(b,c,d)=(4,5,3)または(4,5,3)の2通り
a=3のとき、(b,c,d)=(4,5,2)または(5,4,2)の2通り
a=4のとき、(b,c,d)=(3,5,2)または(5,3,2)の2通り
a=5のとき、(b,c,d)=(3,4,2)または(4,3,2)の2通り よって 2×4=8通り になります。
<Y>について
a,b,c,dに2,3,4,5がどのように並んでも大丈夫。 よって 4×3×2×1=24通り になります。
<Z>について
a=2のとき、(b,c,d)=(4,5,3)または(4,5,3)の2通り
a=3のとき、(b,c,d)=(4,5,2)または(5,4,2)の2通り
a=4のとき、(b,c,d)=(3,5,2)または(5,3,2)の2通り
a=5のとき、(b,c,d)=(3,4,2)または(4,3,2)の2通り よって 2×4=8通り になります。
したがって、(ⅲ)の場合は、 8+24+8=40通り になります。
(ⅰ)(ⅱ)(ⅲ)より、W形の(ア)の並べ方については 11+15+40=66通りとなります。
この66通りは最大の数である7が図1に示すPの位置にあるときであり、7はQの位置に並べることもできるので、 全部で 66×2=132通り となります。
どうでしたか。なかなか大変な作業を要しますが、場合分けして丁寧に集計していけば
何とか求められるものです。
ポイントは、まず7の場所について場合分けをすることです。さらにそれにつながる6の場所が限定されるので6について場合分けをし、最後に最小の1について場合分けをして集計をしていくことです。一言で言えば、数の位置が限定できるものについて、場合分けをしていくということになります。(ア)~(オ)ついて取り組んでいけば、十分な練習ができると思います。
次回は、(イ)について考えていきます。是非、チャレンジしてみてください。
それではみなさん、
またお会いしましょう。