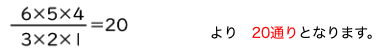こんにちは。
受験Dr.の坂井です。
V形、W形の並べ方についてのお話です。
この2つの並べ方は、考え方が異なるので違いを明確にするためにもセットで学習してほしいと思います。
まずはV形の並べ方について見ていきましょう。
V形に並べるというのはどんな並べ方なのか。それは、数の大きさが大きいほど下に位置し、上に行くほど小さくなるような並べ方です。
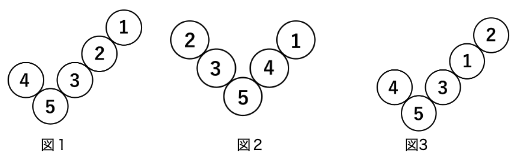
例えば、1~5までの数でVの形に並べると図1や図2に示すような並び方になります。
1から5までの数で最も大きい数が5ですから、5がV形の最も下に位置することになります。
図1ではV形の左側は4ですが、これは4<5だから4は5より小さい数なので5より上側に並べることができます。
V形の右側も5<3<2<1と上に位置するほど数の大きさが小さくなっていきます。
一方、図3を見るとV形の左側が5<3<1までは上に位置するほど数が小さくなっていきますが、1より大きい2が1より上に並んでいるので、このように並べることはできません。
というわけで、V形の並べ方のルールはおわかりいただけたところで、このような並べ方が何通りできるのかを考えていきましょう。
【問題】
1~7までの数をV形に並べる方法は何通りありますか。
まず、どんなVの形があるかを考えていきましょう。
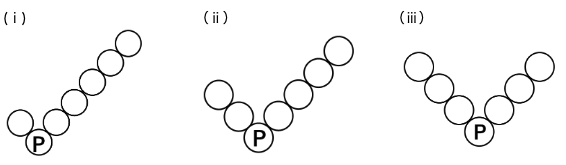
Vの形は、次のような3通りが考えられます。この3通りに場合分けして並べ方がそれぞれ何通りあるかを見ていきます。
(ⅰ)の場合
Pには最も大きい数の7が入ります。Pの左側には1~6までの数のうち、どの数でも並べることができます。右側の数の並べ方は特に考える必要はありません。
なぜなら、左側に入る数が決まれば右側のPを除く5個の数は自動的に決まってしまうからです。
例えば、Pの左側=1であれば1と7を除いた残った数が65432の順にPの右側に並ぶことが自動的に決まってしまうのです。よって並べ方は全部でPの左側=1~6のときの6通りとなります。
そして下図のように左右逆の場合も考えられるので、6通り×2=12通り となります。
(ⅱ)の場合
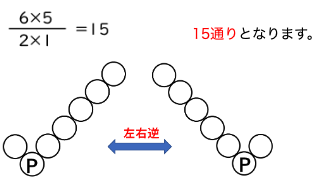
Pには最も大きい数の7が入ります。Pの左側の2個の数は7を除く1~6までの数のうち、2個の数が並ぶことになります。例えば、1<2<P、2<5<Pといったような並び方になります。この場合も左側の並び方が決まれば、右側には左側2個の数と7を除く残りの数が自動的に下側から大きい順に並ぶことになります。よって左側の並び方だけを考えればよいことになります。1から6までの数から2個の数を選ぶ組み合わせを考えればよいので、
15通りとなります。
また、左右逆のVの形も考えると、15通り×2=30通り となります。
(ⅲ)の場合
Pには最も大きい数の7が入ります。(ⅰ)(ⅱ)と同様にPの左側の並べ方が決まれば自動的に右側の並び方も決まってしまいます。ですからこの場合もPの左側の並び方だけを考えていきます。
7以外の1から6までの数のうち、Pの左側に並べる3個の数を選ぶ組み合わせを考えればよいわけです。
(ⅲ)の場合は、Vの形が左右対称となっているため、(ⅰ)(ⅱ)の場合のように、左右逆の場合を考える必要はありません。よって(ⅲ)の場合は20通り となります。
(ⅰ)(ⅱ)(ⅲ)より
12+30+20=62 62通り となります。
V形の並べ方は、Vの形で場合分けしていくことがポイントでした。
次回は W形の並べ方について見ていきます。
それではみなさん、
またお会いしましょう。