こんにちは、算数を担当しています佐々木です。
本日も前回と引き続き、嫌なスウチについてお話していきたいと思います。
今回は、実際なかなか嫌なスウチが消えない問題を使っていきます。
嫌なスウチとは、計算していて途中すっきり割りきれなかったり、分数になってしまったり、素数が
残っている数値とします。
具体的にどういう問題ででてくるのか見ていきたいと思います。
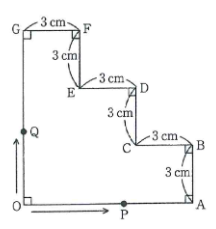
右の図のような図形OABCDEFGがあります。2点PとQは頂点Oと同時に出発します。点Pは辺OA上を一定の速さで往復し続けます。点Qは図の周上を毎秒1㎝の速さで時計回りに進みます。点Pと点Qの速さの比は10:9です。点Pと点Qが出会うまでを考えるとき、次の問いに答えなさい。
出発してから5秒後の三角形OPQの面積を求めなさい。
OGとPQが最初に平行になるのは出発してから何秒後か求めなさい。
点Pと点Qが出会うのは出発してから何秒後か求めなさい。
この中で、
まず、点Pと点Qの速さの比が10:9より、点Pの速さは、10÷9×1=10/9となります。
5秒後なので、10/9×5=50/9㎝、Qは1×5=5㎝
よって、50/9×5÷2=125/9㎠
から、9が分母となる面積になります。
初めの、10÷9の時点で嫌なスウチとなって、これからどんな問題がでるのか不安になってきます。
点が動く問題は、とにかく、角っこに来る時の時間は出しておいた方がいいでしょう。
点QがFにくるのは、3×4=12㎝を毎秒1㎝なので、12秒後。
その時、点Pは10/9×12=40/3㎝
点Aから点Pまでの距離が40/3―3×3=13/3㎝
点Eから辺AOに向かって垂直に引いた線が辺OAと交わる点をIとする
点Pが点Iにきたとき、まだ点Qは、辺FE上にいるということが分かるので、
点Pが15㎝進んだときということわかる。
15÷10/9=13.5秒後
これは、割り切れたので少しほっとします。
点Pと点Qが出会うのは、点Qが辺AO上にいるとき
点Qが点Aにくるのは、27÷1=27秒後
そのとき、点Pは、27×10/9=30㎝
点Pは辺OAを3回行って折り返して3㎝点Aから離れている
点Qは点Pより遅いので、これを追いつくことはない。
よって、点Pがまた点Bまで戻って折り返してくるところとわかる
点Pと点Qが27秒後から合わせて15㎝進むと出会うので、
15÷(1+10/9)=15÷19/9=135/19秒=![]()
よって![]()
となります。
最後も、19がでてきたり、割り切れなかったりと、途中本当に不安になりますが、
これで合っているのです。
考えがしっかりしていれば、途中ででてくる嫌なスウチに惑わされることはありません。
自信を持ってといていけばいいのです。
嫌なスウチ、またどこかで見つけたら載せていきたいと思います。