こんにちは、算数を担当しています佐々木です。

本日は、早稲田中で2012年に出題された問題を取り上げます。

【問題】
A,B,C,D,E,Fは7でないすべて異なる数字です。5けたの数ABCDEを7倍すると6けたの数FFFFFFになります。このとき、5けたの数ABCDEを求めなさい。

FFFFFFFが同じ数値なので、候補としては、
111111か111111の倍数、222222、333333、444444、555555、666666‥‥
①F=1とすると、111111÷7＝15873　　（1と7が利用されているのでダメ）
②F=2とすると、222222÷7＝31746　　（7が利用されているのでダメ）
③F=3 とすると、333333÷7＝47619　　（7が利用されているのでダメ）
④F=4 とすると、444444÷7＝63492　　（同じ4が利用されているのでダメ）
⑤F=5 とすると、555555÷7＝79365　　（7と5が利用されているのでダメ）
⑥F=6 とすると、666666÷7＝95238 〇

となります。

答え.９５２３８

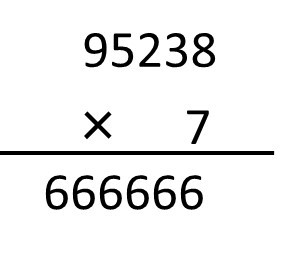
この問題は、かけ算の計算ができる生徒であれば、解くことができます。

方針としては、
Ⅰ．問題を読んで、だいたいどういう数字が出てくるか考える
Ⅱ．調べていく
この２つのステップだけです。
FFFFFFと同じ数字が並び、掛け算をして６桁にしかならない
ということと、
「７ではない」、「同じ数字は使わない」という条件をしっかりと読み取るということができれば、
よいでしょう。

算数の問題を解くときの、方針を立てるということは、
どの問題でも必要なことです。

「だいたいでやってみる」
というのは一見悪いように見えますが、実は良いことなのです。
何も考えず、知っている式に当てはめて解いてしまうより、
「だいたいでやってみる」は、算数の本質を分かっている解き方になります。

そこで大事になってくることが、どの条件をどうやって利用するかということです。

例えば、下のように、文章が長い問題で試してみましょう。
【問題】
ふくろの中に、139個のチョコレートと26個のがキャンディが入っています。これら165個のチョコレートとキャンディを子どもたちに同じ個数ずつ、できるだけ多く分けようと思います。このとき、165個のお菓子をチョコレート、キャンディ関係なく子どもたちに分けたところ、お菓子は12個あまり、あまった12個のお菓子のうち、キャンディは2個でした。子どもの人数が20人以下であるとき、次の問いに答えなさい。

子どもの人数は何人ですか。

文章が長いですが、問題を解くときに利用する文章は、
165個のお菓子をチョコレート、キャンディ関係なく子どもたちに分けたところ、お菓子は12個あまり
この部分だけです。
165－12=153
この153という数字が割り切れる数字、つまり素因数分解して約数を探します。
153＝3×3×17
ここで、余りが12個とあるので、12より大きい数字、17と決まります。

17人いたということがわかったので、（答）17人

問題を解くのかがわかりにくくなるのが、長い文章の問題です。
ここだ！というところを見つけられるようにトレーニングを積んでいきます。

5年生までに○○算の根本原理を入れて、6年生では、どうやって算数の問題に根本原理を利用するのかを一緒に練習していきます。