こんにちは、算数を担当しています佐々木です。

本日は、高さの等しい三角形の見つけ方についてお話いたします。

 

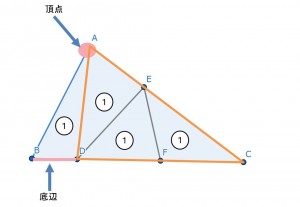
問題：三角形ＡＢＣを下の図のように、3本の直線で面積を4等分しました。

辺ＢＤ：辺ＤＦ：辺ＦＣを求めなさい

 

 

上のような図計を6年生であれば見たことがあると思います。

長さの比を求めなさいという問題になると、

生徒さんたちは、すぐに長さを出そうとして、

三角形の面積の公式底辺×高さ÷2に当てはめようとします。

 

しかし、この問題は一切面積や長さはでていません。

 

ではどのように求めるのか。

 

もう一度問題に戻ると、

どういう情報が与えられているか見てみます。

 

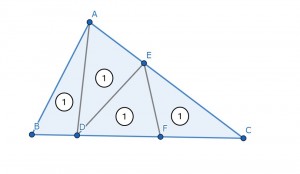
「面積を4等分した」ここがポイントです。

 

面積を4等分したので、面積比は全て１：１：１：１となります。

つまり比を使うしかないということがわかります。

面積比から底辺比を求める

ためには、

↓

高さが等しい三角形を探す

↓

高さが等しいので比べられる

↓

面積比から底辺比が求められる

 

という思考になります。

 

 

ここまでは理解しつつも、

その先に「高さの等しい三角形」を見つけることができない

という症状がでてきます。

 

本日のメインのお話はそこです。

じゃ、どうやって高さの等しい三角形をみつけるか。

 

底辺と頂点を決める

 

これが今日のポイントです。

 

三角形ＡＢＤと高さが等しい三角形はどれでしょうか。

 

まず、三角形は、３つの辺と３つの角度でできているということに

注目しましょう。

 

3つの辺のどこを底辺にしてもいいのです。

しかし、高さが等しい三角形を見つけるときは、

底辺を同じ位置に取らないといけません。

 

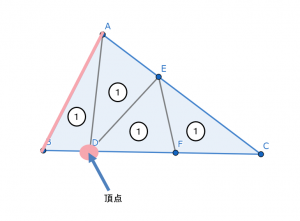
三角形ＡＢＤの底辺を例えば、辺ＡＢとします。

高さを決める「頂点」は、点Ｄとなり、

 

 

頂点から底辺に向かって垂直に下した線が高さ

 

しかし、これだと高さが等しい三角形は見つかりません。

 

高さが等しい三角形は、頂点の1点に集まっているものです。

つまり、

底辺を決めたら、高さが等しい三角形は、

右か左（となり）にしかないのです。

その右か左を底辺として、頂点の1点に集まっているものを見つけます。

 

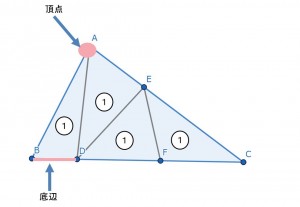
底辺をＢＤにすると、

頂点は点Ａ

 

点Ａに集まっていて、底辺が右か左に

あるもの

 

を探します。

 

 

底辺をＤＣとし、頂点Ａに集まっているものは、

三角形ＡＤＣとなります。

 

辺ＢＤ：辺ＤＣ＝①：③となります。

 

更に、辺ＤＦと辺ＦＣを求めたいので、

高さが等しい三角形を同じように探すと、

 

 

三角形ＥＤＦと三角形ＥＦＣが頂点Ｅに集まっている

高さの等しい三角形となります。

 

辺ＤＦと辺ＦＣは１：１

 

よって、先ほどの

辺ＢＤ：辺ＤＣ＝①：③と

辺ＤＦと辺ＦＣは１：１

をあわせて連比すると、③＝２となるので、6にそろえて、

辺ＢＤ：辺ＤＦ：辺ＤＣ＝２：３：３となります。

 

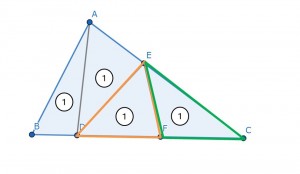
同じように、

辺ＡＥ：辺ＥＣも求めることができます。（答えは一番下の行にあります）

 

ぜひトライしてみてください。

高さの等しい三角形は、

 

まず底辺を決めて、頂点を見つける

頂点の1点に集まっている三角形を見つける

高さの等しい三角形は右か左にしかない

 

今日のポイントは以上3点です。

 

答えは、辺ＡＥ：辺ＥＣ=1：2となります。