こんにちは。算数を担当しています佐々木裕子です。

本日は、特別な○○進法についてお話し致します。

先日授業の時に、この問題がわからないと質問がありました。

上の問題は、8進法の問題です。
普段使われる整数は1の位に0～9の10個の整数です。
4と9が使われない整数の列ということは10個中2個の整数が利用できないので、
0～7の8進法となり、この場合、4と9が抜かれるので、
0、1，2，3，5，6，7，8の8進法です。

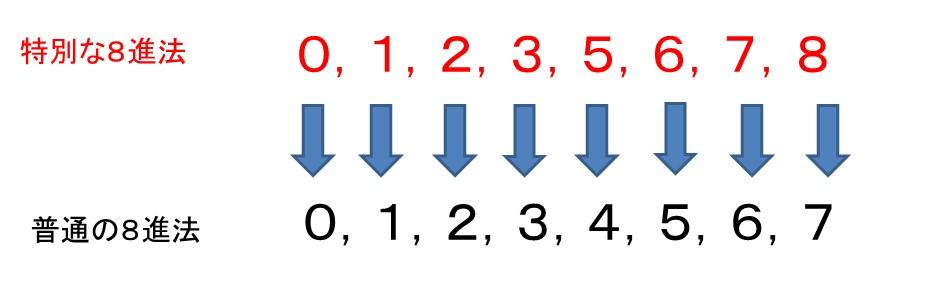
普通の8進法に使われる整数は⇒0，1，2，3，4，5，6，7、
この問題の特別な8進法に使われる整数は⇒0，1，2，3，5，6，7，8
です。
特別な8進法では、数字が順番に出ないということになります。
ということは、もはや、数字ではなく記号であると考えたほうが簡単です。
ただ、問題を解くときは、普通の8進法に戻して計算しないとずれてしまいます。
ここがポイントです！

特別な○○進法は普通の○○進法に戻して計算！

（1）777⇒666に戻します。
6×64＋6×8＋6×１＝438番目ということが分かります。

（2）2021番目⇒2021÷512＝3…485
485÷64＝7…37
37÷8＝4…5
5÷1=5
よって、3745⇒これを特別な8進法で使われている数字に直します。
3745⇒3856となります。

特別な数字が使われている○○進法を普通の○○進法に一旦もどしてから
問題を解くということが必要になります。

もう少し掘り下げてみると、これは、
数字でなくてもいいのです。

例えば、
☆、〇をつかう3進法の問題でも同じです。
0，1，2という普通の3進法の問題を、0は0、1は☆、2は〇に変換するということです。

☆☆〇と表された数字は何番目でしょうかという問題があるとします。
☆は1、〇は2に普通の3進法で使われる数値に戻してあげると、
112となり、これは、9×1＋3×1＋1×2＝9＋3＋2＝14番目ということがわかります。

では、
問題①　〇☆〇は何番目でしょうか。
問題②　25番目はどんな記号で表されるでしょうか。

○○進法は、暗号にも使われるとても面白い考え方を利用した数字です。
スパイになった気分で、いろんな数字を作ってみましょう！
数字じゃなくてもいいのです。記号でもいいんです。

問題①の答え
〇⇒2、☆⇒1を表すので、普通の3進法に直すと、212となり、
9×2＋3×1＋1×2＝18＋3＋2＝23番目

問題②の答え
25番目は、25÷9＝2…7　　7÷3＝2…1　1÷1＝1
よって221⇒○○☆

となります。

予習シリーズでは、
6年上「第2回　数と規則性(1)」必修例題6、練習問題【6】などででてきます。
一度、自分で解いてコツをつかみましょう！

佐々木先生のもっと詳しいプロフィールや指導法はこちらへ！
https://www.chugakujuken.com/juku/prokoushi/sasaki/