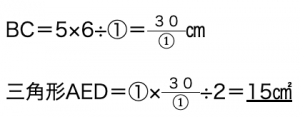こんにちは。算数を担当しています佐々木裕子です。

本日は、図形問題について考えていきたいと思います。

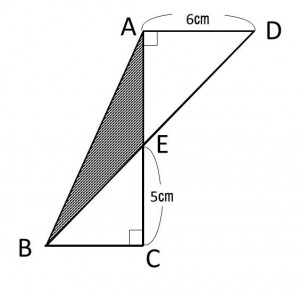
問題：下の図の斜線部分の面積を求めなさい。

この問題の解法は、いくつか考えられます。

まずは
等積変形の利用
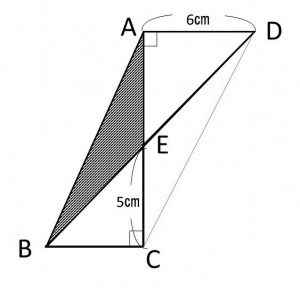
CとDを結び補助線を引きます。

辺ADと辺BCは直角マークがあるので、平行です。
平行線の中で等積移動させます。
三角形ABC＝三角形DBC・・・辺BCは底辺で変えずに、頂点の点Aを点Dへ移動
三角形EBCは共通部分なので、三角形ABEと三角形DECは等しくなります。
三角形DECの底辺をECとすると、高さは、辺AD
よって、5×6÷2＝15㎠

となります。

本日は、それを更に、他の解き方がないか考えてみます。

5年生後半になると、比を学ぶので、比を利用して解けないか考えてみましょう。
比を利用した解き方は2つあります。
辺を①とおいて解く場合と、
相似形の利用です。

まず【別解1】で、辺を①とおく解き方を示します。

【別解1】

AE＝①とおきます。比の①とおきます。
三角形AED＝三角形ACD―三角形ECD
＝6×(5＋①)÷2―6×①÷2
＝30÷2＋⑥÷2―⑥÷2
＝15
⑥÷2は、打ち消しあって消えます。
実は、AEを適当に比の①とおいても解けます。
ということは、比の①ではなく、勝手に4㎝などとおいても
実は解けるということです。

次に、相似形の利用です。

【別解2】

おそらくこの図形を見たときに、
パット相似形があることに気づいた生徒さんも多いのではないでしょうか。
しかし、6㎝に対応する辺がわからない！
5㎝に対応する辺もわからない！
比がでない？！
となり、相似形の利用をあきらめてしまったのではないでしょうか。

大丈夫です！

相似形の考え方を利用して解けるのです。

別解1と同様に、
AE＝①とおくと、
ADとBCが平行なので、三角形AEDと三角形CBEは相似形です。
相似比は、5：①となり、①：5＝6：BCとなります。
そうすると、

が約分されて消えます。

そのため、①という仮に置いた数値が消えて、面積を求めることができます。

これからは、等積変形に気づけなくても、相似形で解けます！

5年生の皆さん、今、比を勉強していますね。
比は「仮に置ける」ので便利なんです。
この問題のように、一旦、比で置いてみて、三角形の面積を求めてみましょう。
実は、比の部分が消えて、本当の答えがでてきます。
「仮においてみる」というのは有効な手立てなんですね。

ぜひ、図形問題に限らず、問題を解いているときに、他の解法がないか考えてみてください。
そして、解法をどんどん増やしていきましょう。