こんにちは。算数を担当しています佐々木裕子です。
本日は、「見抜く」ということについてお話ししたいと思います。
「問題を解ける」、「解き切ることができる」ということは、
どんな問題が出ても、何を使うかがわかり、「見抜ける」からではないでしょうか。
では、その「見抜く」とはどういうことか。
例えば、
85÷34+143÷26=□
という問題が出たときに、どこを見抜けばよいでしょうか。
ひたすら計算してゴリゴリ出していく「必殺技」を使いますか。
まずは、何か潜んでないか疑ってみましょう。
85は5で割ると17がでてきます。34も17で割れるので、
26は2で割ると13がでてきます。そうすると、143も13を持っているのではないかと
疑います。
計算も、ただ前から素直に計算するのではなく、何かワナがあるのではないかと
疑ってから解きましょう。
では、次の問題はどうでしょうか。
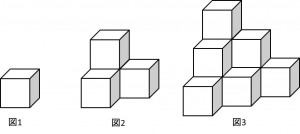
下の図のように、あるきまりにしたがって1辺1㎝の立方体を積んでいきます。
図1には1個、図2では4個、図3では10個の立方体が積まれています。
このきまりにしたがって7段積んだ立体に使われている立方体は全部で何個でしょうか。
1段積んだとき、1個
2段積んだとき、2段目に置かれている立方体は、1+2=3個 1+3=4個
3段積んだとき、3段目に置かれている立方体は、1+2+3=6個 4個+6個=10個
ここまでいくと、立方体の総数が3個ずつ増えているので、
3の倍数ずつ増えるのではないかと思った人は多いのではないでしょうか。
しかしながら、
4段目を調べてみると、
4段積んだとき、4段目に置かれている立方体は、1+2+3+4=10個 10個+10個=20個
となります。つまり9個増えるのではなく、10個増えるのです。
では、
5段積んだとき、5段目に置かれている立方体は、1+2+3+4+5=15個 20個+15個=35個
6段積んだとき、6段目に置かれている立方体は、(1+6)×6÷2=21個 ←三角数!
35+21=56個
7段積んだとき、7段目に置かれている立方体は、(1+7)×7÷2=28個 56+28=84個
この問題を「見抜く」ためには、慎重さも大事であるということです。
安易に4段までの和が3個ずつ増えているからと言って3の倍数と考えてはダメです。
「見抜く」ためには、「もしかすると、こうなのでは」と仮説を立てる必要があります。
では、最後に、次の問題はどう「見抜けば」いいでしょうか。
問題:
異なる量の水が入った3つの容器A、B、Cがあります。ここに、同じ量の食塩を加えよくかき混ぜたものを、食塩水A、B、Cと呼ぶことにします。
食塩水A、B、Cについて、次の①~③がわかっています。
-
食塩水Aと食塩水Bを混ぜると、食塩水Cと同じ濃度になる。
-
食塩水Bと食塩水Cを混ぜると、食塩水Aの2倍の濃度になる。
-
食塩水Aと食塩水Cを混ぜてできる食塩水と、食塩水Bに600gの水を加えてできる食塩水は、同じ濃度になる。
という文章があったとき、どこを見抜けば解けるのか。
まず、①から、
AとBを混ぜるとCの濃度と同じということから
→同じ重さの食塩が入っているので、それぞれの食塩の量を①とすると、
A+B=①+①=②の食塩、Cは①の食塩
ということから、見抜きポイントです!!
食塩水の量の比も2:1とならないと、濃度が等しくなりません!
②からは、
BとCを混ぜると、Aの2倍の濃度となることから、
→食塩の量が、B+C=①+①=②、Aが①の2倍の濃度なので、
食塩水の重さは1:1 食塩水の量が同じで、食塩の重さが2倍にならないと濃度は2倍になりません。ここも見抜きポイントです。
以上から、AとBとCの食塩水の量の比が求められます。
A+B:C=②:①
B+C:A=1:1
全体の量は等しいので、
(A+B)+ C=②+①=③
(B+C)+ A=1+1=2
③ = 2
これを6にそろえて、
A:B:C=3:1:2
となります。
Bの食塩水の量を求めるには、
③より、AとCを混ぜると、(①+①)÷(③+②)の濃度
Bは、食塩水の量が①+600gになるので、⑤=(①+600)×2
⑤=②+1200g
よって、①=400g
B=400gとなります。
この問題では、
①の条件から、AとBを混ぜたときとCの食塩の量の比が2:1だから、
食塩水の量の比も2:1になるということが見抜けたでしょうか。
また、
②の条件からは、BとCを混ぜたときに、Aの濃度の2倍になるということから、
食塩水の量は、1:1とならないといけない。
以上の部分を「見抜けること」が「解けるかどうか」の分かれ目になります。