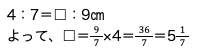こんにちは。算数を担当しています佐々木裕子です。

前回「見抜く」ポイントについてお話ししました。
今回は、更に具体的に、どこを見抜くのかについて話を進めたいと思います。

たとえば、
現在5年生、夏の学習が終わり「比」が出てきて、「比」を利用する
文章題、図形問題を習っているところ、という状況であったとします。

そして、この問題が出てきた時に、どう対処するか。

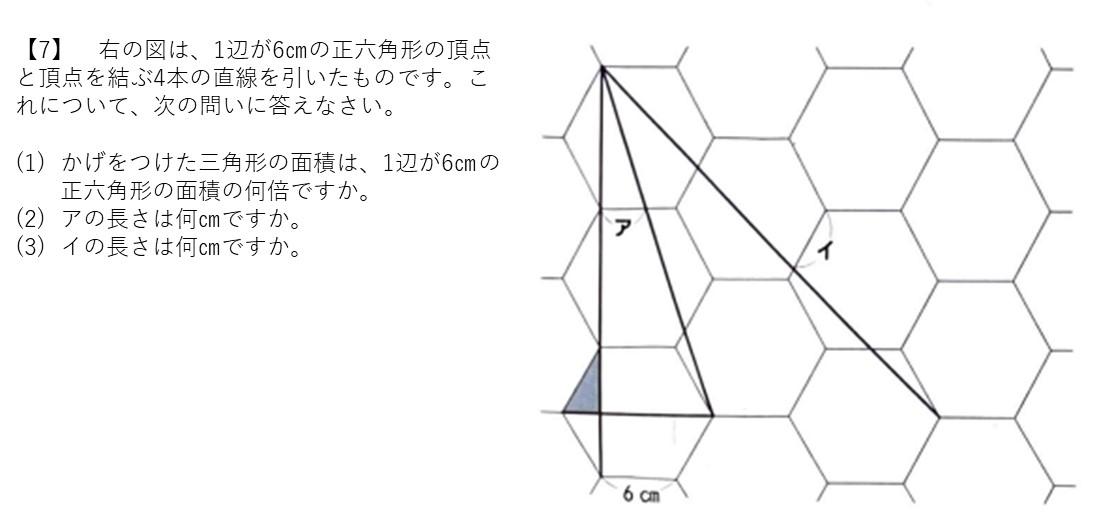
こちらは、実際に2022年度11月、四谷大塚　5年生組分けテストで出題された問題です。

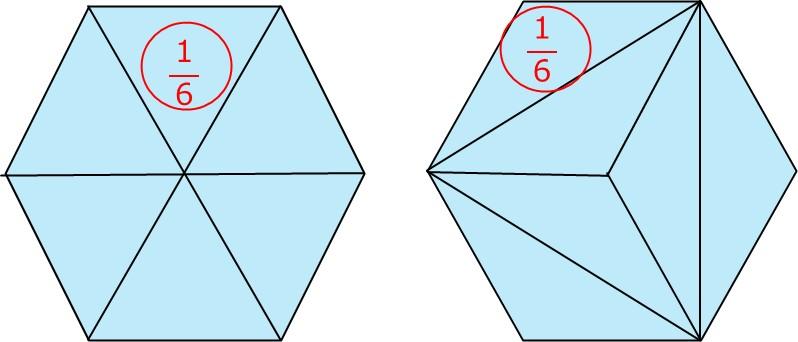
(1)は、正六角形分割です。正六角形の内部を分割すると、

主に、この2種類の分割があります。
これを基準に考えれば簡単です。

となります。
(2)、(3)は、辺の長さを求める問題なので、
相似形を発見しましょう！

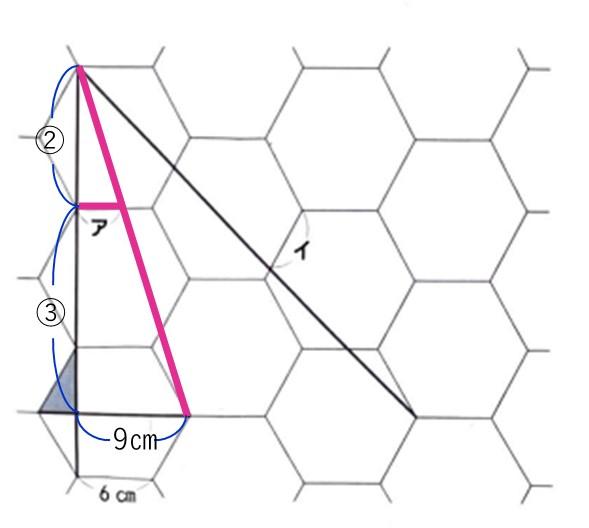
アを求めるので、アを使った三角形と相似な図形を探します。
相似形は平行線の中にあるということを忘れずに。

2：5＝ア：9㎝
よってア＝3.6㎝

次に、

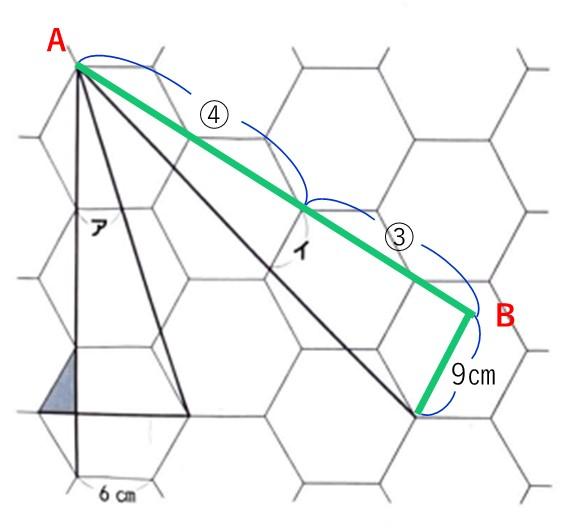
イを求めるときに、直線ABを発見できるかがポイントとなります。

ABの線を引いて、斜めになっているイを求めることができる相似形を探すことになります。
相似形は平行線があるところに存在するので、
平行線を見つけることから始めます。
平行線は、正六角形の一辺を利用します。

ABの直線は、正六角形の対角線上になり、比率が分かる線になりました。

ポイントは、
正六角形分割と相似形となる線を引くことです。

ただ、まだ比を学んで数か月で、この「直線AB」の線を見つけることは
難しいと考えます。
6年生の11月であれば、これは出来てほしいところですが、
5年生のこの時期であれば、まだできなくても許されるでしょう。
この問題を解き切った生徒さんは、おそらく「相似形という性質」と「正六角形の性質」を理解し
その性質を使って探すことができるようになっているのでしょう。

・正六角形の中に正三角形がある
・相似形は平行線の中にある
・正六角形の対角線は正三角形の一辺の2つ分
・ピラミッド相似、クロス相似
など、これらの要素を瞬時に頭の中において、解き進めることができるようになることが大切です。

よって、
この問題の「見抜くポイント」は、
相似形をつくるために直線ABが引けるかどうか
ということです。

算数の勉強方法としては、
一つ一つの要素を探すトレーニングと、複合的になった要素を探すトレーニングが必要です。

どのタイミングでどのくらいの量でということがそれぞれ生徒さんによって違います。
だから個別が必要なのです。