こんにちは。算数を担当しています佐々木裕子です。

本日は、「作図」について、お話ししたいと思います。

 

図が動くと解けない！作図が苦手という声をよく聞きます。

本日は、動く図形を、動かない点に注目することで、描けるようになる

ということをお伝えいたします。

 

たとえば、

実際の入試問題を使っていきましょう。

 

2023年度渋谷教育学園渋谷大問【1】(6)で出題された問題です。

 

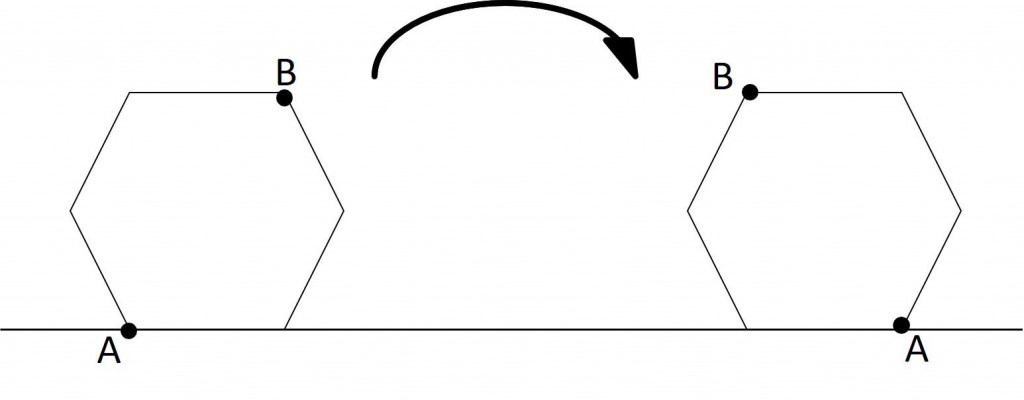
下の図のように、1辺の長さが3㎝の正六角形を、頂点Ａが直線上に戻ってくるまでを滑らずに転がします。このとき、頂点Ａが通ったあとの長さは、頂点Ｂが通った長さより何㎝長くなりますか。ただし、円周率は3.14とします。

 

 

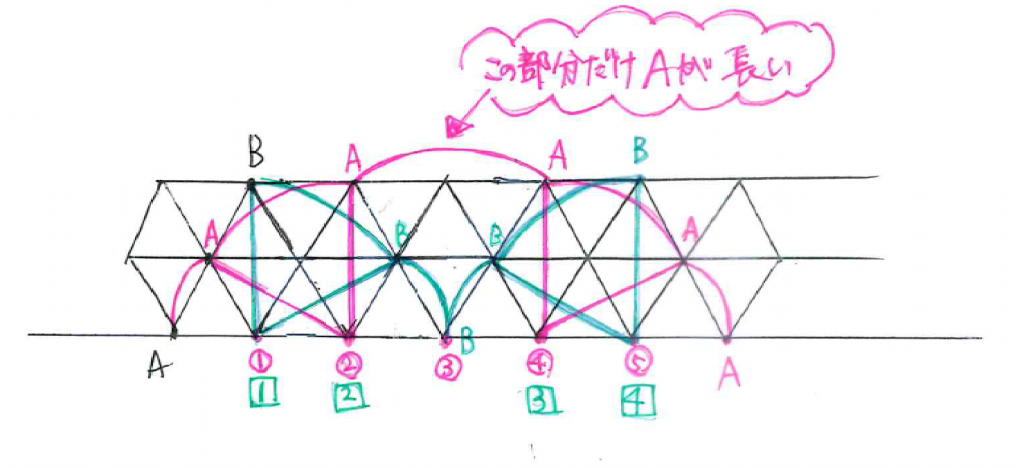
どうなるのか、描いてみました。

①②③④⑤　←Aが動くときの中心

1⃣　2⃣　3⃣　4⃣←Bが動くときの中心

 

①と⑤を中心としたときのAの弧の長さ　＝　2⃣と3⃣ を中心としたときのBの弧の長さ

②と④を中心としたときのAの弧の長さ　＝　1⃣と4⃣ を中心としたときのBの弧の長さ

 

となるため、③を中心としたときのAの弧の長さの分だけ長い

ということがわかります。

よって、

 

これは、図が描ければ解くことができます。

 

図を描くときのコツは、

 

必ず1点に注目することがポイントです。

全体の図を見てしまうと、どこがどう動いているかわからなくなってしまいます。

次に、どこを中心に動いているか、動くときの「動かない」中心を見つけましょう。

 

頂点Aは①～⑤を中心に動いています。

中心が①⑤のとき、半径3cm

中心が②④のとき、半径はわかりません。仮にアcmとします。

中心が③のとき、半径は6㎝

 

頂点Bは1⃣～4⃣を中心に動いています。

中心が1⃣　4⃣のとき、半径はわかりません。しかし中心が②でAが動いた弧の長さと同じです。

中心が2⃣　3⃣とき、半径は3cm

 

つまり、中心がわかれば、半径がどの長さかが見分けがつきます。

そして、動いた角度もどこからどこへとたどることができます。

 

このように、

「動かない」中心、半径、中心角

 

この3点セットに注目することが描くときのコツです。

長方形や正方形など、簡単な図から練習しておきましょう。