こんにちは。算数を担当しています佐々木裕子です。
本日は、
余りに注目して解く問題のお話をします。
例えば、
6509×2+3752×3を11で割った余りを求めなさい。
という問題で、
式を計算してから11で割って余りを出す方法は使わずに、答えを出してみましょう。
式を計算したら、もちろん、答えは出ます。
ただ、もうすこし簡単な方法で出せないか考えてみます。
例えば、簡単な数値で試してみると、
15×3を例えば7で割ると、
45÷7=6・・・3となります。
それを15÷7をして2あまり1となることを利用するのです。
15は7で割ると1余るのだから、15×3というのは、あまりも3倍されるということだと
解釈できます。
余りの1を1×3とし3あまると答えても変わりはありません。
余り1が3回たまるということです。
そうすると、
6509÷11=591…8
3752÷11=341…1
8×2+1×3=19 19÷11=1…8 よって 答えは8となります。
実際に計算をしてみると、
6509×2+3752×3=13018+11256=24274
24274÷11=2206…8となります。やはり余りは8ですね。
つまり、
計算しなくても、それぞれのかかっている数字を11で割ってみて
その時出た余りどうしを足すという考えができます。
東邦大付属東邦中の2021年度の問題にもトライしてみましょう!
6468×2+939×5を13でわった余りを求めなさい。
こちらも、
まずは、6468÷13=497…7
939÷13=72…3
7×2=14 14÷13=1…1
3×5=15 15÷13=1…2
よって、余りの1と2をたします。 1+2=3 答え.余りは3
となります。
余りの性質を使った問題です。ただし、計算が和と差と積のときだけです。わり算のときは使えません。
更に、次のような余りを利用した問題にもチャレンジしてみましょう!
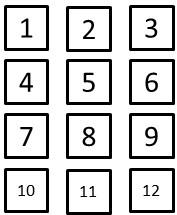
右の図のように、1から12までの数を書いたカードが
1枚ずつあります。この中から3枚のカードを同時に
選びます。このとき、次の問いに答えなさい。(1) 3枚のカードの選び方は何通りありますか。
(2) 5の倍数のカードを1枚だけ含んで、和が3
の倍数になるような3枚のカードの選び方は何通り
ありますか。
(3) 和が3の倍数になるような3枚のカードの
選び方は何通りですか。
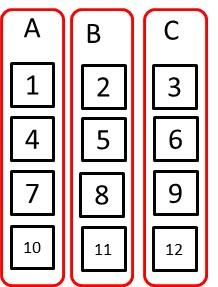
12×11×10÷(3×2×1)=220通り(2) 5の倍数はBグループとAグループに入っています。
Aグループは3で割ると1余る
Bグループは3で割ると2余る
Cグループは3で割るとわり切れるグループです。
・【5】のカードと他2枚の選び方は、
和が3の倍数になるためには、【5】がBグループなので、
余りが2。他2枚は余りが1のAグループから10以外のカード
と余りが0のCグループから1枚をそれぞれ選ぶか、Bから5以外の2枚を選ぶかなので、
3×4+3=15通り
・【10】のカードと他2枚の選び方は、
【10】のカードがAグループの余りが1になるグループなので、
他2枚は、Bグループから5以外の1枚とCグループから1枚ずつ選ぶか、Aから10以外のカードを2枚選ぶかなので、
3×4+3=15通り
よって、15+15=30通り 答え.30通り
(3)和が3の倍数になるような3枚のカードの選び方は何通りですか。
ア. A、B、Cから1枚ずつ
イ. Aから3枚
ウ. Bから3枚
エ. Cから3枚
ア⇒ 4×4×4=64通り
イ、ウ、エはいずれも 4×3×2÷(3×2×1)=4通り
4×3=12通り
64+12=76通り
余りの性質を使った問題を上げてみました。
以上のように、
「余り」を求めるときに、単純に計算して求めるのではなく、式をよくみて
何か工夫できないかを考えてみましょう。
また、3で割ったときに余りが0か1か2になるということを利用した問題を紹介しました。
どこかでまた出てきたときに、ふっと思い出してくれると嬉しいです。