こんにちは。算数を担当しています佐々木裕子です。

本日は、
比を利用した問題に注目していきたいと思います。

5年生は今ちょうど「比」の使い方や「比を利用した問題」を扱っていると思います。
また、6年生は、比を利用した入試問題に直面しています。
比を利用するとはどういうことか、具体的な問題を使って示していきます。

問題：浅野中学　H28年度に出題された問題より

解説

上りと下りの距離の比は、

全体が27なので、27―（9+4）＝14・・・平地の距離

 

 
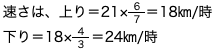
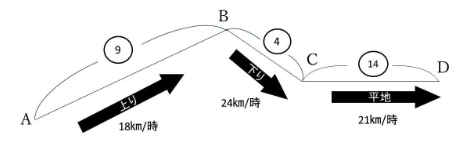
上り、下り、平地の時間の比は、
⑨÷18㎞/時：④÷24㎞/時：⑭÷21㎞/時＝③：①：④
よって、この合計が40分に当たるので、③＋①＋④＝⑧＝40分
①＝5分に当たるので、上りには15分、下りには5分、平地では20分かかっていたことがわかります。

となります。

つまり、
まず、距離の比を求め、そこから距離÷速さから時間を求めていますが、
そのときに、距離は比であり、実際の距離ではありません。
しかしながら、比÷実際の速さ＝比という形をとって、比÷比や比×比を利用しているのです。

比を割ったり、かけたりしています。
それが使えるようになるためには、もともとの速さの意味がわかっていないといけません。
時間を求めているのか、距離を求めているのか、速さを求めているのか、
明確にして「比」を利用していく必要があります。

式の意味がとても大切になってくるということです。

速さを勉強しているとき、3公式をしっかりとマスターしておきましょう。
そうすれば、「比」という抽象的概念がでてきても焦る必要はありません。
「意味」を常に考えて「式」を用いられていれば、大丈夫です。

距離＝速さ×時間
時間＝距離÷速さ
速さ＝距離÷時間

ですね。

比がでてきても、もとに戻って式の意味を考えることが、比を制覇する近道です。

次回も比の利用問題を扱っていきます。