こんにちは、算数を担当しています佐々木です。

本日は、嫌な数値がでてきたときにいかに粘れるか
というお話をしていきたいと思います。

嫌な数値とは、計算していて途中すっきり割りきれなかったり、分数になってしまったり、素数が
残っている数値でしょうか。

割り切れなかったり、整数で答えがでなかったりすると、すぐに手を止めてしまう生徒さんがいます。
割りきれなくても「分数」という手立てがあるのだから、
粘って最後まで答えを出してといつも伝えます。

確かに、気持ち悪い、すっきりしない、自分の答えが間違っているのではないかと
不安になったりします。
それは分かりますが、いつもいつも整数で答えがでるとは限らないということを知っておいて欲しいです。

例えば、桜蔭の問題で、以下のような問題が出題されました。

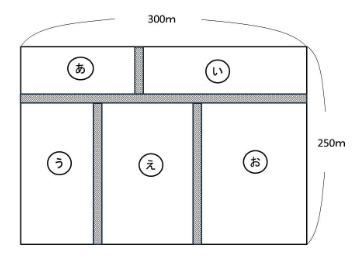
下の図は、長方形の土地を幅3ｍの道(斜線部分)で5つの長方形の土地に分けたものです。あ、い、う、え、おの部分の面積をそれぞれあ、い、う、え、おとします。
あ：い：う：え：お＝１：２：３：４：５となるとき、えの部分の面積を求めなさい。

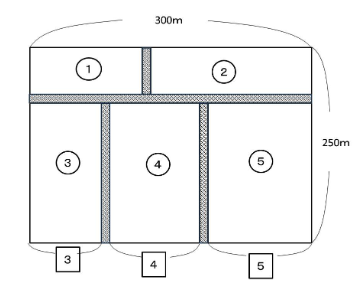
あ、い、う、え、おの部分の面積をそれぞれ①、②、③、④、⑤とすると、下の図のように、
う、え、おの横の長さが3：4：5と表すことができます。

上の図より、えの横の長さを求めると、
300m―3×2＝294mとなります。
それより、4⃣＝294÷(3+4+5)×4＝98mとなります。

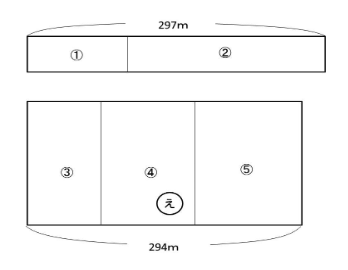
また、上と下の段に分けると、

この途中式に、驚くべき数値が使われています。

2段に分けて考えていくと、まず、あとえのたての長さの比を求めると、
(①+②)÷297m：(③＋④＋⑤)÷294
＝③×294：⑫×297
＝49：198

と意外とすっきりしてきます。

そして、あとえのたての長さの合計は、250－3＝247mなので、
えのたての長さは、
247÷(49＋198)×198＝198m
よって、えの面積は、198×98＝19404㎡

となります。

途中で、294と247の数値が消えず分母に残ってしまうのですが、
上手く約分でき、198、49の数値がでてくるところがすごいところです。

仕組まれてもちろん作られているわけですが、
その数値を選んだところが驚きです。

素数の積では、例えば、29×7＝203とか、29×11＝319、23×11＝253、
23×7＝161などなど、嫌な数値はたくさんあるわけですが、
その中でしっかりと最後わり切れる数値が使われているということに感動しました。

途中はわり切れなくても、最後まで粘れば、この問題は綺麗な整数でもとめることができます。
最後まで粘ることと、分数で一旦表しておくという手立てを持っていることを
忘れないようにしましょう。