こんにちは、算数を担当しています佐々木です。

本日は、出来る問題は完答する。そのためには、どこに
意識を集中しておけばよいかということをお話していきます。

例えば、

問題：右の台形を、直線ℓを軸にして1回転させて
できる立体について、次の問いに答えなさい。（１）体積は何㎤ですか。
（２）表面積は何㎠ですか。

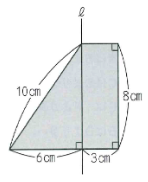
この問題は、解き方は分かっていても完答する
率が極めて少なくなる問題です。
なぜなら、3.14が何回もでてくるからです。

何回も出てくるのであれば、やはり初めから「まとめる」ということを
考えて式を作っていきましょう。
手順としては、

（１）完成図を描く
（２）円柱部分と円すい部分に分ける
（３）比を利用できれば利用する
（４）式を作る
（５）3.14でまとめる

この順番で問題を解き進めていきます。

(1)の体積は、
円柱部分が、3×3×3.14×4＝36×3.14
円すい部分は、比を利用し、
相似比　1：2
体積比　1×1×1：2×2×2＝1：8
となるため、小さい部分の体積を求め、3×3×3.14×4÷3×（8-1）/1＝84×3.14

よって、(36+84)×3.14＝120×3.14＝376.8㎤

表面積が、更に体積より正答率が低くなる問題ですが、
とにかく、部分部分で分けて、「半径」に意識を集中して式を作りましょう。
「３方向から見る」ことが原則です。

上・・・半径3㎝の円
側面・・・母線部分の5センチのところ
側面上・・・円柱の側面積
下・・・半径6㎝の円

3×3×3.14＋6×6×3.14＝45×3.14
円すい台の側面部分
10×6×3.14―5×3×3.14＝45×3.14
円柱の側面
3×2×3.14×4＝24×3.14

まとめると、
(45＋45＋24)×3.14＝114×3.14＝357.96㎠

となります。

この問題を出題すると、いきなり式を書きだす生徒さんがいます。
そうではなく準備が必要です。
まずは、先ほども書いた手順に沿って問題を解いて欲しいと思います。

（１）完成図を描く
（２）円柱部分と円すい部分に分ける
（３）比を利用できれば利用する
（４）式を作る
（５）3.14でまとめる

立体の体積を求めるときも、円柱と円すいにわかれるということを意識する
表面積を求めるときは、3方向から見て、部分部分に分けた図を描くようにしましょう。
また、間違ってはいけないのは、半径です。

「円の半径に意識を集中させる問題」は、
長方形のまわりをすべらず1周する円の問題も要注意です。
角を曲がるときと、直線を動くときの半径は違います。
また、その場合は「半径」と「中心角」も神経を研ぎ澄まして、確認していきます。

それぞれの問題で、どこに神経をとがらせるのか、どこに注意しなくてはいけないのかは違います。しかしながら、神経を注ぐポイントがあるということを意識して問題を解く癖を付けましょう。