こんにちは、算数を担当しています佐々木です。

本日は、
時間差のある旅人算では、時間を一旦勝手に置いてみるとうまくいくというお話を致します。

麻布の2022年度【4】(改題)より

兄と弟の2人が、図のような東西にのびた道で、自転車に乗って競走します。
2人はそれぞれ一定の速さではいあり、スタート地点を変えて何回か競走します。ただし、ゴール地点は毎回変わりません。

初めに2回競走をしたところ、結果は次のようになりました。
・2人がA地点から同時に出発したところ、兄が弟より4.6秒早くゴール地点に到着しました。
・A地点の24m東にB地点があります。弟がB地点から、兄がA地点から同時出発したところ、弟が兄より1秒早くゴール地点に到着しました。

弟の速さは秒速何ｍですか。（(2)が本来ありますが、今回は省略いたします）

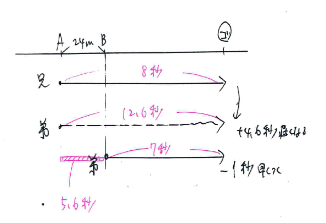
まず、上記の状況図（進行図）を描きます。
弟の速さを知りたいので、具体的な距離と時間がわかるところを探します。
24ｍのところに注目します。
さて、弟はそこにどれだけの時間がかかったのでしょうか。

まず、兄と同じところからスタートすると4.6秒の差ができる。
また、24m兄の前からスタートすると1秒速くなる
ということは、ずらした24ｍ部分が4.6秒+1秒＝5.6秒

となります。

4.6秒と1秒の差を作ったほうが良いのか、和を作ったほうが良いのか迷う人は、
次のやり方も考えてみましょう。

勝手に兄は8秒かかったとします。
そうすると、図に表していますが、弟はＡからスタートした場合、8＋4.6秒＝12.6秒かかったことになります。また、Ｂ地点からスタートした場合は、8－1＝7秒かかったことになり、
12.6―7＝5.6秒と分かります。

これは、兄を8秒でない時間に勝手に置いても、問題のポイントは変わりません。
12秒かかったとしても、A地点から同時にスタートした時の弟はその4.6秒+12秒＝16.6秒
また、弟はB
地点からスタートした時、12-1＝11秒としても16.6―11＝5.6となり、24mにかかる時間は5.6秒と決まります。

このように、算数では、勝手に置いて解いてよい問題があります。

比の問題などは特に、勝手に置いて解くという問題です。
また面白い問題がでてきたら次回お伝え致します。