こんにちは。算数を担当しています佐々木裕子です。
差集め算の根本原理は、
【同じ人数、同じ個数で比べる】ということです。
本日は、3問用意しますので、どのレベルまで自分が到達しているか、レベルチェックしてみましょう。
レベルⅠ・・・初級 根本を理解している
レベルⅡ・・・中級 偏差値50-55
レベルⅢ・・・上級 偏差値60以上
レベルⅠ
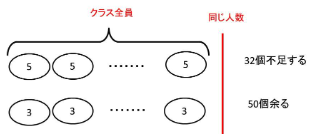
問題:アメをクラス全員に配ります。1人に5個ずつ配ると32個不足し、1人に3個ずつ配ると50個余ります。1人に4個ずつ配ると□個余ります。
同じ人数で比べているので、32個不足するのと、50個余るところに差が集まってきます。
32+50=82
82÷(5-3)=41人であるとわかります。
アメは41×3+50=123+50=173個 全部のアメの数
4×41=164個必要なので、
173―164=9個 余ります。
答え.9個
レべルⅡ
問題:
2500個のキャンディがあり、生徒全員に1人3個ずつ配ると500個以上余りました。そこで、その余った分を1人に1個ずつ配ると、もらえない生徒が80人以上いました。生徒全員の人数は何人以上何人以下ですか。
「何人以上、何人以下」という言葉があると、その時点で終了-!と
あきらめてしまう生徒さんが多いのですが、
なぜ何人以上、何人以下となるかを考えましょう。
500個以上余るということから、
2500―500=2000個以下を配ったと推測
これを3個ずつ配っていくので、
2000÷3=666…2 より 666人以下と考えられます。
また、余った分を1人に1個ずつ配るということは、
1人に4個ずつ配っているということになるので、
2500+80=2580個以上、キャンディは必要となります。
2580÷4=645人以上
答え.645人以上666人以下
レベルⅢ
問題:
ある映画館には、座席が20列あり、各列の座席数は同じです。開場前に、何人かの客が入場を待っています。入場した客は必ず列の左端から座っていきます。間に1つの席を空けて座ると右端の座席は空席になり、間に2つの席を空けて座ると右端の座席には客が座ることになります。
次の問いに答えなさい。
(1)1列の座席は、何席あると考えられますか。考えられる座席数は小さいほうから4つ答えなさい。
(2)最前列から順に、間に1つの席を空けて座るとちょうど最後の2列がすべて空席になり、間に2つの席を空けて座ると、24人が座れません。入場を待っていた客は何人ですか。
(3)最前列から順に、間に1つの席を空けて座り、何列目からか間に1つの席を空けて座った列は何列ですか。
差集め算の根本原理は、「同じ○○で比べる」ということです。
座席の20列というのは変わらないので、座り方が変わるということに注目して解いていきましょう。
(1)
間が1つ
間が2つ
のそれぞれの場合で考えていきます。
間に1つの席を空けて座ると右端の座席は空席になるので、
1列に座る人数は2の倍数となります。
間に2つの席を空けるときは、
1,4,7,10,13,16・・・の番号の席に座ります。
3の倍数+1の人数が考えられます。
この2つの条件を満たすのは、
4、10、16、22となります。
(2)
座席数ごとに、1列に座る人数を調べると、
・4席だった場合、2人となり、明らかに合いません。
・10席だった場合、1つ空きの場合、10÷2=5人 18列×5=90人
2つ空きの場合、10÷3=3…1 1列に4人座ることになるので、20×4=80人 となり、
条件は90-80=10人となり×
・16席だった場合、1つ空きの場合、16÷2=8人、18列×8=144人
2つ空きの場合、16÷3=5…1、1列に6人座ることになるので、20×6=120人
144―120=24人で条件に合います。
・22席だった場合、1つ空きの場合、22÷2=11人、18列×11=198人
2つ空きの場合、22÷3=7…1、1列に8人座ることになるので、20×8=160人
198-160=38となりこれも条件に合いません。これ以上の席数であると、差が24人よりも
更に増えていくのであり得ない。
よって、1列の座席数が16席の場合、条件に合うので、144人
(3)
(2)より、座れなかった24人を「1つ空き」の席に座らせていくということになるので、
24÷(8-6)=12列
答え.12列
レベルⅠは、鎌倉学園2019年度第1次の問題でした。入試問題でも、やはり根本を聞いてきますね。また、レベルⅡは慶應普通部2021年度,レベルⅢは城北埼玉2021年度からの問題です。レベルⅡ,Ⅲは根本がわかっていて、更に、
問題文を正確に読み取り、どのようになっているか場合分けを自身でやっていくという
手立てが必要になります。
「こうだったら、どうなるのか」と推察しながら、条件を当てはめていくという作業が要求されます。
レベルⅠだからと言って簡単ではありません。差がどこにあつまるのか、差に注目し、同じ人数で比べるのかということが見抜きポイントとなります。
5年生の予習シリーズ第4回は「いろいろな差集め算」です。
どこに注目するのか練習を積んで、入試問題にもチャレンジしてみましょう。