こんにちは。算数を担当しています佐々木裕子です。
本日は、「比の作り方」についてお話したいと思います。
①Aの4倍とBの3倍が等しいとき、A:Bは?
②Aの4倍とBの3倍とCの5倍が等しいとき、A:B:Cは?
③Aの![]() 倍とBの
倍とBの![]() 倍が等しいとき、A:Bは?
倍が等しいとき、A:Bは?
④Aの![]() 倍とBの
倍とBの![]() 倍とCの
倍とCの![]() 倍が等しいとき、A:B:Cは?
倍が等しいとき、A:B:Cは?
①の答えはA:B=4:3ではありません。
このミスが多いです。
まず、「等しい」という言葉に注目することが大事です。
「Aの4倍」の「の」は「×かける」になおして、A×4=B×3となります。
等しいので何か適当に4でも3でも割れる数字つまり、4と3の最小公倍数12と置いてみます。
A×4=B×3=12
そうすると、A=12÷4=3、B=12÷3=4となり、A:B=3:4となります。
つまり、逆のかかっている数字をもってくれば、3:4となるということですね。
次に、②で比べる数字が3つになった場合どうでしょうか。
先ほどの要領で、逆にすればいいというのが、3つだと成り立ちません。
つまり、A:B:C=5:3:4というように右から左を左から右に移したのでは求まりません。
どうしたらいいのでしょうか。
まず、やはり「等しい」に注目して、
A×4=B×3=C×5
という式をつくります。ここでも「等しい」ということを利用し、
4でも3でも5でも割れる数字→4と3と5の最小公倍数60を持ってきます。
A×4=B×3=C×5=60
A=60÷4=15、B=60÷3=20、C=60÷5=12
となります。よって、A:B:C=15:20:12です。
それでは、③のように分数になったらどうでしょう。
A×![]() =B×
=B×![]()
A:B=![]() :
:![]() =
=![]() =3:4としてしまうミスが多いです。
=3:4としてしまうミスが多いです。
そうではなくて、
等しいということから、
A×![]() =B×
=B×![]() =1
=1
ここで、1と置いたのは、どちらでも割り切れる簡単な数だからです。
そうすると、A=1÷![]() =4 B=1÷
=4 B=1÷![]() =3となり、
=3となり、
A:B=4:3となります。
つまり、![]() と
と![]() の逆数の比になっています。
の逆数の比になっています。
逆数とは、分母と分子を入れ替えた分数のことです。
④は、比べる数字が3つになったときです。
しかしながら、これも逆数の比になるので、
A×![]() =B×
=B×![]() =C×
=C×![]() =1
=1
として、A:B:C=![]() =8:6:5
=8:6:5
となります。
ここまでみてきたように、①②は、かかっている数字の最小公倍数、③④は、分数なので、1と置いて
逆数の比でというように問題によって解き方を変えて答えを求めました。
ただ、それぞれの問題で見つけるべきものを変える(最小公倍数にしたり、逆数にしたり)のは、
問題を解く時に判断する力も必要になってきます。
そうではなくて、もう少し簡単にできないか。
一つ紹介しておきます。
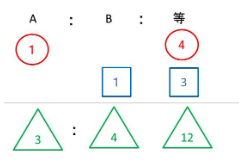
A、B、等(しい)と書き出す方法です。
①Aの4倍とBの3倍が等しいとき、A:Bは?
A:B:等と書いた下の段にそれぞれ言われていることを書いていきます。
「等」というところは、等しいので、4と3が等しくならなくてはいけません。
4と3の最小公倍数12とおきます。
それに伴って、Aは3倍、Bは4倍して下におろします。
そうすると、A:B=3:4とでてきます。
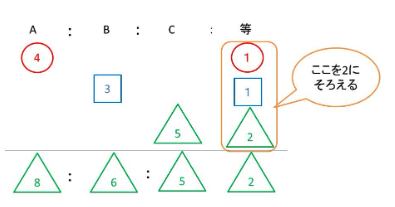
このように④もやってみると、
④Aの![]() 倍とBの
倍とBの![]() 倍とCの
倍とCの![]() 倍が等しいとき、A:B:Cは?
倍が等しいとき、A:B:Cは?
よって、答えは、A:B:C=8:6:5となります。
こちらのやり方の方が、整数、分数、小数になっていても汎用性がきくのではないでしょうか。
まとめると、
1.最小公倍数や1と置いて逆数の比
2.「A:B:等」と置いて連比
の2つのやり方を紹介しました
どちらでも答えは導けます。
自分が慣れた方がいいと思います。
目的は、〇をもらえる方法で解くということです。
どちらの方が自分にとって解きやすいか、一度解いてみてください。
自分が書いた解答に〇がもらえるようにミスのリスクを減らすことを考えていきましょう。