こんにちは。算数を担当しています佐々木裕子です。

本日は、立体の体積、水量問題で、長さや時間を求めるときは、約分形式を使う
ということについてお話いたします。

体積を求める式は、
①底面積×高さ
と
グラフから求めるときは、
②□㎤/分×△分　（単位は、LやｍL、時間、分、秒など変わります）

この2つがあります。

 

 

この直方体の体積は、底面積×高さになりますね。
具体的には、

 

 

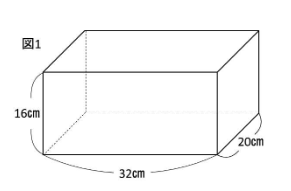
図1のように、たて20㎝、横32㎝、高さ16㎝の直方体の体積は、
20×32×16となります。

この容器に、水を10㎝までいれたとすると、

 

 

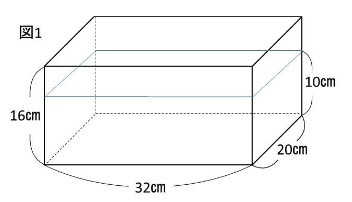
水の体積は、
20×32×10となります。

これに、更にグラフがでてくると、

 

 

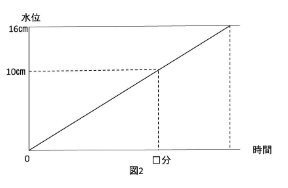
毎分2Lの割合で、水をそそいでいくと、10㎝になるのは、何分何秒ですか。
という問題が出てきたします。

これを解く時に、2L＝2000㎤なので、
20×32×10＝6400
6400÷2000＝3.2分＝3分12秒となり、
今のように、一つ一つ計算して求めてもいいのですが、
6400を求めるときに、20×10＝200と計算して
2000で割るので、200の計算をしなくても、割り切ることができます。

つまり、

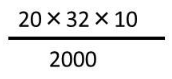
この分数の形にして、約分したほうが楽で計算ミスのリスクは減るのです。

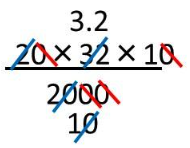
＝3.2＝3分12秒です。

体積を求めなさいという問題では、もちろん、底面積×高さになると思いますが、
高さや時間を求めるときに、一旦体積は式だけの形に置いておいて、
約分するという形をとってみましょう。

計算して答えを出すという方法に慣れている小学生は、
なかなかこの「約分形式」がしっくりこない生徒さんもいます。
具体的な数が出てこないと、イメージできないということがあるかもしれません。

ただ、体積の数値は大きな数値になる可能性が高いです。
０が4個ついたり、3個ついたりします。
また、わり算のところで、われるかどうかがみつけられず時間がかかってしまうということが
おこります。

折角やり方はあっているので、このような「約分形式」にするというテクニックが分かっていれば、
計算に時間をかけず、リスクも小さくてすみます。

体積から長さや時間を出す問題は、約分形式を取り入れて練習してみてください。

計算方法から見直していくという考え方です。
体積計算や水量グラフの問題は、なかなか内容も難しくなってきて、
根本が分かっているのかどうかテストの点数だけでは判断できないところがあります。

根本は理解しているのに点数が取れなかったというときの原因の一つとしては、計算方法で間違っている場合があります。
この場合は、約分形式を取り入れるという修正になってきます。

どの部分でのミスなのか、細かい部分をみて、そのミスに合った修正を施していくことで点数を確実に伸ばしていくことができます。