こんにちは。算数を担当しています佐々木裕子です。

本日は、半径のでていない円の面積について考えていきます。

2024年度　神戸女学院中学部の問題です。
図1のように、長方形ABCDの頂点B、Cを中心として半径が辺BCの長さに等しい2つのおうぎ形をかき、この2つのおうぎ形の交わる点をEとします。この点Eと長方形の4つの頂点A、B、C、Dをそれぞれ結んだとき、図2のような辺の長さと角の大きさになりました。点Eを中心として三角形ABEを1周させたとき、辺ABが通った部分の面積を求めなさい。

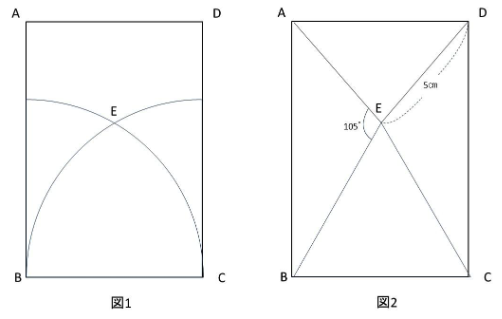
点Eを中心に三角形EABを回転させるので、
点Eからの遠い点、近い点をまず見つけます。
点Eから一番遠い点は、点B
点Eから一番近い点は、点Eから辺ABに向かって垂直に下した線との交点です。その交点を
Fとすると、EFの長さとEBの長さを求める必要があります。

長方形ABCDは、たても横の長さも出ていません。

図1と図2が与えられているだけです。
では、どうすればEFとEBの長さが求められるのでしょうか。

EFとEBの長さはは求められません！

「長さがでてこないけれど、円の面積は出せる」
という言葉でピンとくるでしょうか。

そうです、「半径×半径」さえわかればいいのです。

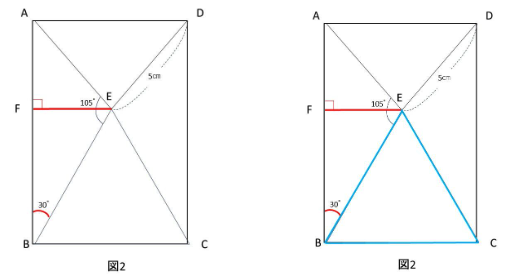
Eから垂直に線を引きその直線とABとの交点をFとします。
EFは角EFB＝90°になります。
また、三角形EBCはBCが円の半径、EB、ECもそれぞれ円の半径なので、辺の長さが
すべて等しくなり正三角形とわかります。

そうすると、角FBE＝30°となり、
辺EF＝①とすると、辺EB＝②となります。

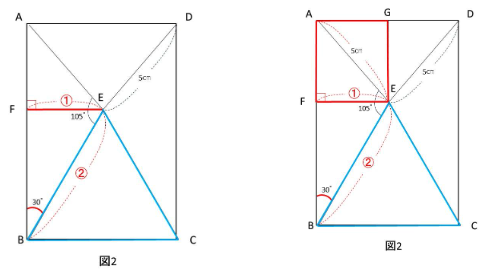
AFEGは角FAE＝180―(30°＋105°)＝45°となり、辺AF＝辺FEとなるので、正方形。
よって、
①×①＝5×5÷2＝12.5

②×②＝①×①の4倍となります。
　　 ＝12.5×4＝50

②×②×3.14―①×①×3.14＝（50―12.5）×3.14＝37.5×3.14＝117.75㎠

となります。

この問題で、見抜くべきポイントは、
・半径×半径がでてこない
・正三角形がある
・正方形がある
・30°ときたら30°60°90°より辺の比が1：2となる
・中心から一番近い点、一番遠い点

です。

この5要素を見つけられるか、使いこなせるかが解けることの条件となります。
一つ一つのポイントは分かっていると思います。それを入試問題では組み合わせて今回の問題のように
出題されます。一つ一つのポイントをまず6年生夏前までにインプットし、それらのポイントを
入試問題でも見つけられるようにしていきます。そして、この9月から6年生は過去問に入っていき、今までの積み重ねたポイントを見抜ける様にしていきます。