こんにちは。算数を担当しています佐々木裕子です。
本日は、動く図形・動く点の問題についてお話いたします。
「動く図形」「動く点」の問題と言っても、1つではありません。
点が動く
- 1点が動く→長方形を動く、三角形を動く、平行四辺形を動くなど
- 2点が動く
- 2点の出会い算・追いかけ算
- 面積を2等分
- 平行になる
- 垂直になる
- 周期・規則性
などが、考えられます。
平面図形が動く
- 四角形の外側を円が動く
- 四角形の内側を円が動く
- 四角形の外側を三角形が動く
- 正六角形の外側を正三角形が動く
- 正六角形の内側を正三角形が動く
- 平行移動
- 線上を転がりながら動く
まだまだ、これ以外にも「動く図形」「動く点」の問題を細分化することができると思います。
なぜ細部化する必要があるかというと、
このように細分化していって、どの段階で躓いているのかを把握するためです。それぞれの生徒さんで躓く場所は違ってきます。どこまではできて、どこからできないのか、どの図形になるとできていないのかを正しく把握することが大切です。
そして、躓いている問題を類似問題でトレーニングしていきます。
10月からは、9月に解いた過去問を見ながら、それぞれの学校の特徴を踏まえて、どの分野で躓いているのかを把握し、テーマを決めてトレーニングしていきましょう。
ここ最近で、動く図形、動く点の問題で、おっと思った問題がありましたので、
そちらを紹介します。動いたあとの図形が描けるかやってみましょう。
淑徳与野2021年度第1回
【5】
次の図のように4cm離れた平行線ℓとmの間に、半径4cm,中心角135°のおうぎ形P、Qがぴったりはさまっています。おうぎ形Pを直線mに沿って矢印の方向に移動させます。ただし、おうぎ形Qは動きません。あとの問いに答えなさい。
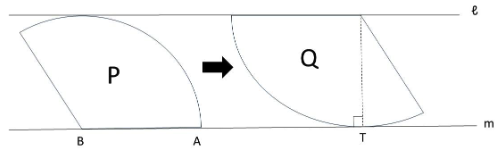
(1)点Aと点Tが重なったとき、おうぎ形PとQの重なった部分の面積は何㎠ですか。
(2)点Bが点Tと重なったとき、おうぎ形PとQの重なった部分を斜線でぬりなさい。
(3)(2)の斜線部分の面積は何㎠ですか。
解説
点Aが点Tと重なると、下の図のようになります。
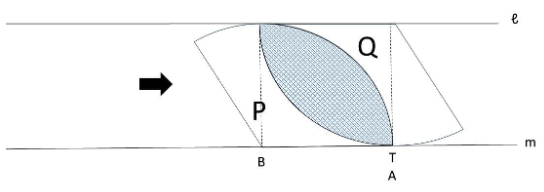
重なった図形は、半径4㎝のおうぎ形2つが重なった「葉っぱ」形になっているので、
(4×4×3.14×1/4―4×4÷2)×2=9.12㎠となります。
点Bと点Tが重なった図形は、下の図のようになります。
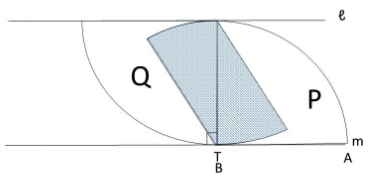
(3) 135°-90°=45°のおうぎ形が2つできます。
その面積なので、4×4×3.14×1/8×2=12.56㎠
です。
動いた後の図がわかれば、求める図形の面積は簡単です。
このように、動く図形の問題をテーマ別にトレーニングし、作図の練習も積み上げていきましょう。
図を描くときの注意点は、なるべく正確に描くことです。
大きくずれた図を描いてしまうと、求める線の長さや面積が見つけられなくなる可能性があります。
フリーハンドで描くので難しいですが、なるべく正確に描きましょう。
鉛筆を使った方がすべらないのでうまく描けます。
円を描くときは、力を抜いてフワッと描くとうまくいきます。
問題を解くために必要な図形を描くことを心掛けましょう。




