こんにちは。算数を担当しています佐々木裕子です。

本日は、「ミス」についてお話したいと思います。

最近、発見したのは、問題を解いていて途中でミスをするということも多くあるのですが、
それよりも、式の一番最後！でミスをしてしまう生徒さんが多いということです。

ミスの原因は、さまざまな要因が考えられます。

計算問題のミス

①数値の見間違い
②たし算・ひき算の繰り上がり、繰り下がりミス
③計算の順番の間違い
④約分・通分の間違い
⑤逆算で計算の順番の間違い
⑥工夫を知らない
⑦特殊な計算方法を知らない

大問の中での計算ミス

①文章中の数値の見間違い
②問題文の読み間違い

でしょうか。
今回は、この「大問中での計算ミス」を確認していきたいと思います。

恐らく、原因は、問題を解く上で「これでいいのかな、合ってるかな」と
不安に思いながら解いているからだと思います。
自信を持って解いている生徒さんもいると思いますが、神経がいろんな方向に行っていて、
それで、ふっと最後の最後に気が抜けて最後の式でミスをしてしまうということもあるのではないかと思います。

それを防ぐには、もちろん、自信をつけて余裕を持って解くことですが、
そんな簡単に自信というのはつくものではないので、他にないかと考えてみました。

まずは、図を描いたり、式を書いたり、自分を落ち着かせるための武器を持っておくことです。

それでは、情報を整理するために、「紙に書いておく」ことです。
頭の中で処理するスピードも大切ですが、あとで使う情報もあるかもしれないので、紙に書いておくのです。せっかく問題用紙があるので、用紙のスミを使って書いておくと、目で見えて、頭の中が整理できます。

例えば、女子学院中　2015年度　【5】で出題された問題です。

お楽しみ会で子どもにりんご、みかん、かきの3種類のくだものを配ったら、次の❶～❽のようになりました。下の□にあてはまる数を入れなさい。
❶　全員がくだものを少なくとも1種類はもらいました。
❷　りんごとみかんだけをもらった人は9人います。
❸　りんごとみかんをもらった人は16人います。
➍　みかんとかきをもらった人は11人います。
❺　くだものをちょうど2種類もらった人は21人います。
❻　りんごだけをもらった人の数は、かきだけをもらった人の2倍です。
❼　りんごをもらわなかった人の数は、かきをもらわなかった人の数の半分です。
❽　みかんをもらわなかった人の数と、かきをもらわなかった人の数は同じです。
3種類のくだものをもらった人は□人、みかんをもらった人は□人、子どもは全部で□人います。

この問題を頭の中だけで処理して解ける人っているのでしょうか。もしかするといるかもしれません。
ただ、脳の中って見えないし、どこに置いておくのか、どうやって頭の中だけで解いたのか、もしいたとしても、私は、理解できません。すごい頭脳の持ち主なんだなと感心するだけです。

まず、「みかんとりんご」とか「りんごとかき」など重なりがあるなと判断すると、
ベン図というものがあります。
ベン図を描きます。

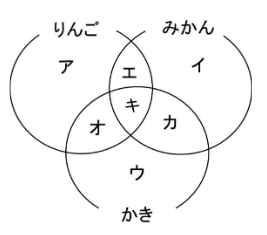
このベン図にそれぞれ❶～❽で言われていることを整理して書いていきましょう。
そうすると、まず❻より　ア＝ウ×2とわかりア＝②、ウ＝①と置くことができます。❷と❸から、キの3種類のくだものをもらった人は7人とわかります。
❽より、8+①＝9＋イ　よって、イ＝①－1とあらわせます。次に❼より、（①－1）＋4＋①＝②＋3が、②＋9＋①－1＝③＋8の半分なので、
（②＋3）×2＝③＋8となり、④＋6＝③＋8、よって④－③＝8－6、①＝2人と分かります。

みかんをもらった人は、9＋7＋1＋4＝21人
こどもは全部で、21＋8＋2＋4＝35人となります。

このように、後は図を描いて条件にしたがって埋めていくだけです。

スペースを使って図を描いて頭の中を整理です。
「書いておいておく」ということを試してみてください。