こんにちは。算数を担当しています佐々木裕子です。

本日は、速さと比についてお話いたします。

5年生の夏以降「比」の学習が進んでいると思いますが、受験算数で重要になってくる単元の一つとして「旅人算と比」が挙げられます。

等しい部分を探そう
①距離が等しい
②時間が等しい
③速さが等しい

まずはこの３つに注目して解き進めます。
１　距離が等しい
例えば、学校から駅まで分速60ｍで行く場合と、分速80mで行く場合、速さの比は60:80＝3：4です。時間の比は、3：4の逆比で4：3になります。速さが速い人ほどもちろん時間は短くなるという理屈と、時間は、距離÷速さで求めるので逆比になります。
つまり、距離が等しい時、速さと時間は逆比になります。

２　時間が等しい
例えば、太郎君と花子さんがAとBの2地点間を、太郎君はAからBへ、花子さんはBからAへ同時に出発したとき、4分後に出会ったとすると、出会うまでの時間が同じで、太郎君は200m、花子さんは120m進んだとすると、距離の比が200:120＝5：3となり、速さの比も5：3となります。
つまり、時間が等しい時、距離の比＝速さの比となります。

３　速さが等しい
この場合、太郎君がA地点から300m離れているB地点まで40秒かかったとすると、150mには距離が半分なので、時間も20秒となります。つまり、速さが等しい時、距離の比＝時間の比となります。

それでは、等しい部分がないときはどうするのか。
異なる比でも、比×比、比÷比は利用できます。

具体的に問題で見ていきましょう。
問題：学習院女子

A地点とB地点を結ぶ1本のまっすぐな道があります。夏子さんは7時にA地点を出発して、毎分180mの速さで2地点間を2往復走りました。冬子さんは7時3分にA地点を出発して、毎分72mの速さでB地点まで歩きました。冬子さんは途中でB地点から帰ってくる夏子さんと出会い、さらにそこから480mの地点で夏子さんに追い抜かれました。これについて、次の問いに答えなさい。
(1)冬子さんが帰ってくる夏子さんに出会ったのは、A地点から何mのところですか。
(2)A地点とB地点は何mはなれていますか

問題文に則して、進行図を描きましょう。

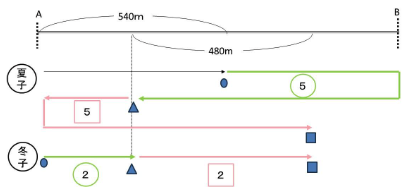
2人の速さの比は、180：72＝5：2となります。
ピンク色のところに注目すると、時間が等しいので、5：2となります。
[2]＝480mに気づけば、
[2]＝480、[1]＝240m
よって、[5]＝1200m　1200m―480m＝720mこれは、A地点から出会った地点までの2個分なので、
720÷②＝360m
答え：360m

(2)緑に注目すると、ここも時間が等しいので、5：2となります。
今度は、②＝360mなので、⑤＝900m
900＋360＋540＝1800m　これは、AB間2個分となるので、
1800m÷2＝900m
となります。
答え：900m

「時間が等しい」ということを利用して解き進めました。
出会った地点から追いつくまでの時間が等しいので5：2、
7時3分から出会うまでの時間が等しいので5：2

それぞれ時間は違いますが、夏子さんと冬子さんがそれぞれ動いた距離は、5：2となります。
時間が等しいとき、速さの比＝距離の比
が利用でき、距離を求めることができるのです。

図で言うと、ピンクのところと、緑のところに注目できるかが解くカギとなります。

まとめると、

①進行図を描き
②等しいところを探し
③比を利用する

この3ステップです。
進行図は、進行グラフと迷うときもありますが、行ったり来たりして止まっている時間があれば、「進行図グラフ」の方がいいと思いますが、比の利用をしたいときに、「どこが等しいか」を見抜きやすいのは、「進行図」だと思います。線の長さが同じ、時間が同じ（同時刻マークを付けて）であることが解くカギとなるためです。
比を利用できるように図の描き方も練習していきましょう。