こんにちは。算数を担当しています佐々木裕子です。
本日も「見抜く」力について、更に見ていきたいと思います。

こちらは、算数オリンピック2021　キッズBEEファイナルで出題された問題です。

問題：
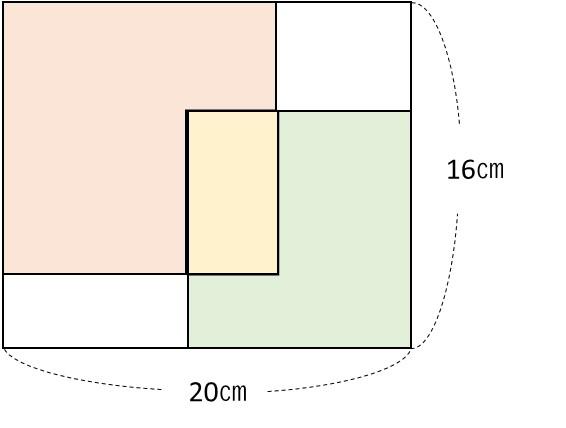
図のように、たて16㎝、よこ20㎝の大きな長方形の中に正方形を2つ重なるように書きました。すると、新しくできた3つの長方形のまわりの長さはすべて同じになりました。
(1)　正方形が重なっている部分の周りの長さは何㎝ですか。
(2)　正方形が重なっている部分の面積は何㎠ですか。

(1)は、簡単でしょうか。
3つの長方形を確認し、その長方形のたて、横の長さをそれぞれたすと、
全ての和が、20㎝が2本と16㎝が2本できるので、
(20＋16)×2＝72
3つの長方形のまわりの長さは等しいので、72を3で割ると一つ分の長方形のまわりの長さになります。
72÷3＝24㎝

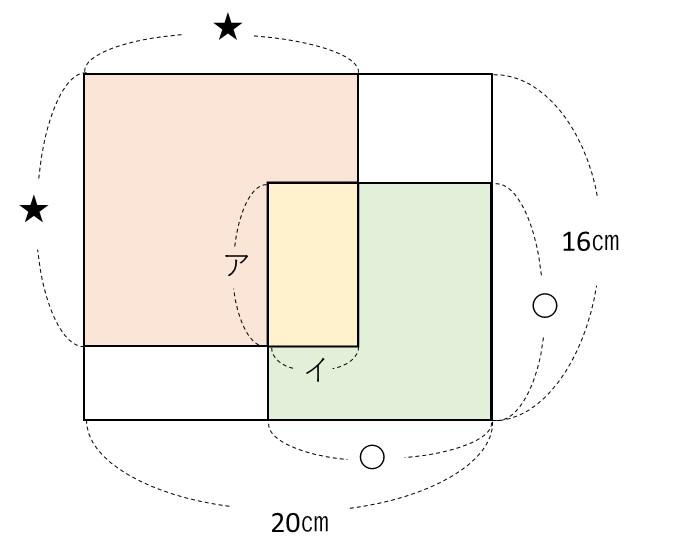
次に(2)は、ピンクの正方形の1辺を★、みどりの正方形の一辺を〇とおいて、
重なっている分の長方形のたてをア、よこをイとします。

これは、式を利用するという考えが必要になり、3年生にとっては、
やや難しいテクニックになります。
一旦、求める答えとは切り離して、等しいということを利用した式を作ることが
出来るかが問われています。

与えられている情報をもとに、論理的に式を作って解いていくことが求められています。

では、次に、式やテクニックというよりも、柔軟な思考が必要である問題です。

問題：

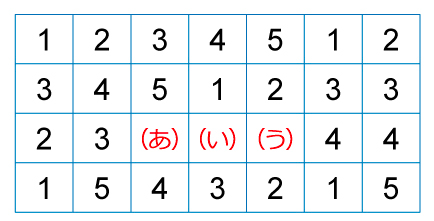
あるルール通りに数字が書いてあります。
(あ)、(い)、(う)に入る数字を答えましょう。

算数オリンピック2019　キッズBEE　トライアル

こういう問題を出題すると、
大人は、列や行で規則性、等差数列やグループに分けるなどいろいろ知っているので、
どれかな？と当てはめていきます。ただ、その考えだとこれは求めることができません。
そうではなく、柔軟な発想です。

ある生徒さんにこの問題を出したところ、
10秒くらい考えて、1の出てくる回数、2の出てくる回数、3の出てくる回数、
4の出てくる回数、5の出てくる回数を数え始めました。
そういう発想か！と思い感動しました。

確かに、回数の差に何かヒントが隠されているかもしれません。
全体を見渡すことができているなと感心しました。
細部を見ることも大事ですが、全体を見渡して何か言えることはないかと
考える発想はすごく新鮮でした。

そうです。これは、全体を見て、
ぐるぐる回っている！ということに気付けばいいのです。

(あ)＝2、(い)＝1、(う)＝5
こういった問題は、テクニックというよりも柔軟な発想ですね。
ぐるぐる回っている
ということに気付くということです。

全体を見渡すこと

今回のポイントをまとめると、

①与えられた情報をもとに論理的に式にする視点
②全体を見渡せる視点
この①②の両方を持つことです。