こんにちは。
算数科のSです。

今回のテーマは「面積を2等分する考え方」です。

線対称や点対称な図形では簡単に面積を2等分することはできますが、
今回は凹凸がある図形を扱います。

さっそく、面積を2等分する図形を見てみましょう。

特に長さの指定はないので、面積を求めながら考える問題ではありません。
図形の特徴をうまく使って上の図形を2等分するのです。

図形の特徴とは何を指すのか、そのヒントは「点対称な図形の面積を2等分する方法」にあります。

ここでいったん上の図から離れて、長方形と平行四辺形の面積2等分のお話をしましょう。

上の図のように長方形や平行四辺形は対角線の交点を通る直線で分割すると、面積が2等分されます。
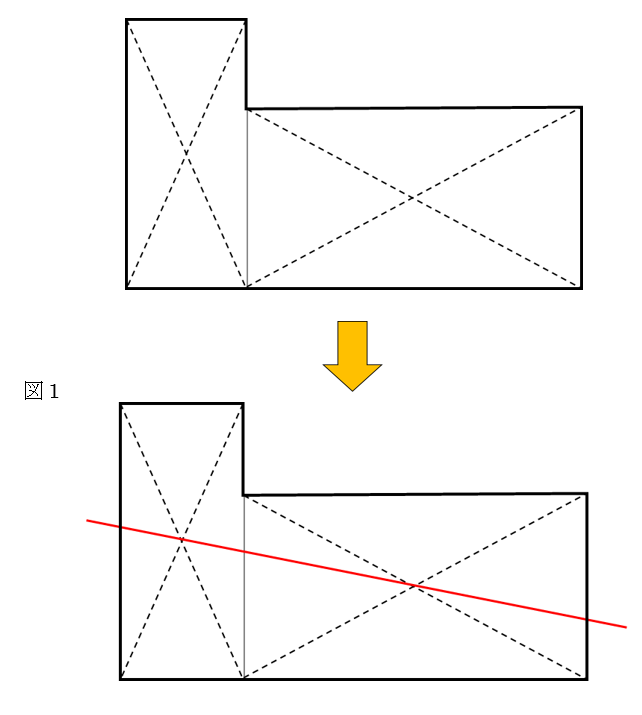
この特徴を使うと図1のような凹凸がある図形でもうまく2等分することができます。

ここでもう一度最初の図を見てみましょう。
この図形の中に長方形を見出すことができますか？

そうです、1本線をひいて下図のように2つの長方形に分けることができます。
それぞれの長方形の対角線の交点を見つけ、その交点を通るような直線で分割すればよいのです。
すると下図1のような2等分線がひけます。

「ん？自分が想像していたのとは違う図だな・・・」と思われた方もいらっしゃるのではないでしょうか？
そうです、この問題の答えは１つではないのです。

もう１つの図は浮かびましたか？
答えは下図2になります。

なるほど！と思ってもらえたら幸いです。

しかし！これで終わりではないのです！！！

もう長方形に分ける方法はないと思っていませんか？
確かに、「中に」作るのはこれだけです。

「中」じゃなければ「外」ってことになりますね？
凹凸をうまく使いましょう！

最後の方法は下図3です。

いかがでしたか？
面積を2等分するおもしろい考え方をご紹介しました。

いろいろな図形で試してみるとおもしろいかもしれませんね！
それではまたお会いしましょう！