皆さま、こんにちは！

 

前々回からつるかめ算についてのお話をしています。
今回はその第３弾です。
前回は、つるかめ算をどう解くか、その処理について考えてみました。
つるかめ算にはいろいろな処理の仕方があります。
その中でも、もっとも原始的な表を作って書き出す、という方法を前回は確認しました。
地道な解き方ですが、こういった作業を面倒くさがったり、おそろかにしたりしてはダメですよ、とお伝えしました。
今回は、つるかめ算の解法の定番中の定番、面積図についてです。
おそらく、多くのお子さんがつるかめ算の解法として身につけているのは、この方法ではないでしょうか？

 

ではまず、簡単なつるかめ算の問題を面積図で解いてみましょう。
次の問題を考えてみてください。

 

 

まず問題を見たときに、これがつるかめ算だということを必ず確認しましょう。
前々回に説明したように、つるかめ算の本質は「２種類の合計が出てきている」ということです。
今回はどうかというと、合計本数の１５本と、合計代金の１３２０円という、２種類の合計が出てきていますね。
ということで、これは間違いなくつるかめ算の問題です。
わかりきったことでも、こうやって意識して確認しておくことが、より複雑な問題を考える際に役に立ってきます。

 

次に、面積図でこれを解いてみましょう。
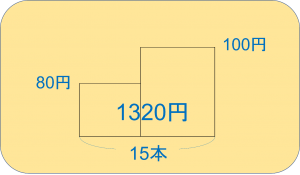
たての長さをそれぞれ１個の代金、よこの長さをそれぞれの個数として、２つの長方形を並べてみます。
すると、以下のような図ができます。

 

 

このとき、全体の面積が合計代金の１３２０円を表しています。
このあとは、この図を上下に分けるか、それとも左上の欠けている部分に注目するか、２つの方法があります。
今回は、後者の方法で行ってみましょう。

 

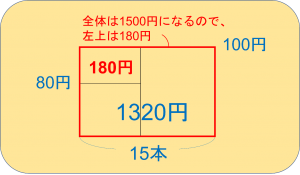
まず、左上の欠けている部分を補って、全体を大きな長方形としてみます。
すると、全体の面積は、１００×１５＝1500となります。
実際には1320円ですから、左上の欠けている部分の面積は180円分ということになります。

 

 

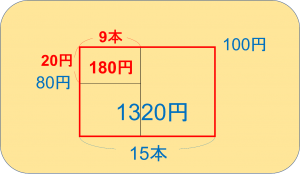
この部分のたての長さは、80円と100円の差の20円なので、180円を20円で割れば横の長さが出ます。
180÷20＝９で、これが鉛筆の本数にあたるということになります。

 

 

ということで、答えは、鉛筆が９本、ボールペンが６本ということになります。
このときに、必ず答えを問題文にあてはめて確認するクセもつけておきましょう。
鉛筆９本とボールペン６本なら、合計金額は８０×９＋100×６＝1320で、1320円です。
ちゃんと問題文を満たしています。
暗算でも構わないので、ひと呼吸おいてチェックするだけで、ミスを減らせます。

 

さて、ここで大切なことは、面積図が意味していることは何か？ということです。
たての長さを１本あたりの金額、横の長さを本数ということにしているわけですが、面積はたて×横です。
ということは、この場合は、１本あたりの金額×本数ということで、面積は合計代金を表しています。
これも、当たり前のようでも、いつも意識しておいた方がよいポイントです。
なぜかというと、これが理解できると、面積図は様々なものに利用可能だということがわかるからです。
２つのものの積で表せるような関係は、すべて面積図で表現可能なのです。
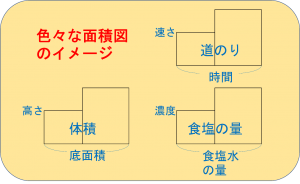
例えば、速さ×時間＝道のり、ですよね。
ということは、たての長さに速さをとって、横の長さに時間をとれば、面積は道のりを表します。
また、濃度（の百分の一）×食塩水の量＝食塩の量、ですよね。
ということは、たての長さに濃度をとって、横の長さに食塩水の量をとれば、面積は食塩水の量を表します。
あるいは、高さ×底面積＝体積、ですよね。
ということは、たての長さに高さをとって、横の長さに底面積をとれば、面積は体積を表します。

 

 

このように、２つのものの積に関する問題というのは、すべてが面積図で表現可能なのです。
ということは、こういった問題を解く際にも面積図は利用できるということです。
実際に、食塩水の混ぜ合わせの問題では、面積図を書いて解くことができます。
また、立体の水量変化の問題も、面積図（この場合は正面図と呼ばれますが）を書いて考えることが基本です。
ということで、この面積図という考え方は非常に応用範囲が広いのです。
単につるかめ算が解ければ良いと考えずに、その意味しているところまでしっかり考えておくことが大切です。

 

ちなみに、この問題は前回説明したように表を書いて解くことも、もちろんできます。
また、これも前回解説したように、片一方にそろえてから変化を考えて解く、ということもできます。
ためしに、後者のやり方で解いてみましょう。
まず、15本すべてが100円のボールペンだったとします。
すると合計金額は100×１５＝１５００で、1500円になりますね。
しかし、実際には1320円だったので、180円多くなってしまっています。
そこで、100円のボールペンを、何本か80円の鉛筆に変えることを考えます。
鉛筆の方が1本あたりの金額は低いわけですから、合計金額も減るはずです。
100円のボールペンを80円の鉛筆に変えると、その差の20円だけ合計金額も減ります。
いまは180円減らしたいので、180÷２０＝９で、鉛筆を９本にすればよいとわかります。
鉛筆が９本なら、ボールペンは１５－９＝６で、６本となりますね。
ここでも、念のため確認です。
鉛筆９本とボールペン６本なら、合計金額は８０×９＋100×６＝1320で、1320円です。
ちゃんと問題文を満たしていますね？
ということで、鉛筆９本とボールペン６本が正解です。

 

さて、ここで何かに気がつきませんか？
先ほど解いた面積図の処理と、いま解いた処理の仕方は、実はほとんど同じことをやっています。
全体の面積を1500円と考えたことは、すべて100円のボールペンだったら？と考えるのと同じことです。
また、実際との差の180円というのは、面積図で言うと左上の欠けた長方形の部分を求めています。
そして、この欠けた長方形のたての長さ２０というのは、ふたつの金額の差です。
さらに、どちらの解法も、最終的に180÷２０＝９という計算をしています。
まったく同じですよね！
つまり、面積図は、片一方にそろえてから変化を考えて解く、という解法を図で示しているとも言えるのです。
ですから、どちらの解法も本質的にはやっていることは同じで、解き方として大きな差はないということです。
このように２つの解法を捉えられるなら、より深くつるかめ算を理解していると言えるでしょう。

 

ということで、たったひとつの問題でも、様々に見方を変えれば、色々な解法を学ぶことができます。
また、一見は違って見える解法も、よく考えてみれば同じこと、ということがあることもわかります。
勉強の理想は、一を聞いて十を知る、です。
しかし、それができるためには、様々な知識や解法の間に、共通点や違いを考える習慣が必要です。
「これとこれは何か似ているなー」とか「ちょっと違うけど、この差が実は大きいのだなー」とか考えてみましょう。
そういったことを繰り返していくと、新しいことを学ぶ際に、それを理解するスピードが上がっていきます。
そして、すべてを説明されなくても、その問題や解法の本質ということに、自分で気が付けるようになってきます。
いわゆる「応用力」いうものの正体は、おそらくこういうことだろうと思います。
たかがつるかめ算と甘く見ずに、そこからいくつものことが学べるということをぜひ知っておいてください。

 

では、また次回お会いしましょう！